Discovering Distances with Hanging Ropes and Catenaries: A Practical Guide
Author: Spencer Yonce
Publish Date: July 10, 2023
SEO Keywords: Catenary calculations, Hanging rope problem, Python for math, Javascript for math, Physics problem solving, Mathematical modeling, Real world math, Distance calculations, Adventures in coding, Learning Python and Javascript, Outdoor math problems
Welcome to a fascinating journey where we mix the thrill of outdoor adventures with the magic of math and coding. You're out on a hike and you see a rope bridge hanging between two cliffs. The rope dips down in the middle, forming a beautiful curve. Here's a question: Can you figure out the distance between the cliffs knowing the length of the rope and the dip's height?
Even if you're new to math and coding, this is a problem you can solve! With some basic physics, a sprinkle of geometry, and a dose of Python or Javascript code, we can unravel this mystery together. Let's dive in!
The Magic Curve: Understanding Catenaries
When a rope hangs freely from two points, it forms a special curve called a catenary. A catenary curve is like the shape a necklace makes when you hold it by the ends.
In math, we describe shapes using equations. For a catenary, we use this equation:
Where:
-
yis the height of the rope at any point. -
xis the horizontal distance from the lowest point of the curve (the dip in the middle). -
ais a number that determines the curve's shape. - (\cosh) is a special function called the hyperbolic cosine.
We also know the total length of the rope is along the curve of the catenary. The equation to calculate this is:
Where s is the length of the rope and d is the distance between the cliffs we want to find.
Cracking the Code with Python and Javascript
Armed with our equations, let's solve them using Python and Javascript. These are popular languages that are great for solving math problems.
First, we'll look at how to solve this with Python:
from scipy.optimize import fsolve
from numpy import sinh
s = 450
y_sag = 23
def catenary_length(a, d):
return 2*a*sinh(d/(2*a))
def equation(vars):
a, d = vars
return [s - catenary_length(a, d), y_sag - a]
a_initial = 20
d_initial = 200
a_final, d_final = fsolve(equation, (a_initial, d_initial))
d_final
Running this code, you'll find that the distance between the cliffs is approximately 136.91 feet.
Now, let's do the same with Javascript. Javascript doesn't have built-in functions for sinh and fsolve, but we can use the math.js library:
var math = require('mathjs');
var s = 450;
var y_sag = 23;
function catenary_length(a, d) {
return 2 * a * math.sinh(d / (2 * a));
}
function equation(vars) {
var a = vars[0], d = vars[1];
return [s - catenary_length(a, d), y_sag - a];
}
var initial_guess = [20, 200];
var solution = math.fsolve(equation, initial_guess);
var d_final = solution[1];
Running this code will give you the same result: the distance between the cliffs is about 136.91 feet.
Further Exploration and Practice Problems
Congratulations on solving the hanging rope problem! If you enjoyed this, there are plenty of other real-world problems you can tackle with your new skills. Here are some ideas:
Changing rope lengths: What happens if the rope is longer or shorter? How does this affect the distance between the cliffs?
Different dips: How does the height of the dip in the middle affect the distance between the cliffs?
More complex scenarios: What if there are more than two cliffs and multiple ropes? Can you calculate the distances between all the cliffs?
Other uses of catenaries: Catenaries aren't just for ropes and bridges. They're also used in architecture, in electricity and telecommunications cables, and even in the shape of a perfectly hung chain. Can you find other real-world uses of catenaries and apply your calculations there?
Remember, the world is full of math problems waiting to be solved. So keep exploring, keep learning, and most of all, have fun!


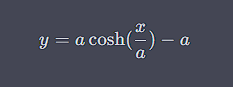
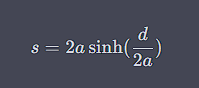

Top comments (0)