Falsification of randomness and transformation by sorting of pseudorandom sequences. Priority of Russia
Objective: to prove possibility of falsification of chance and reality of overcoming rigged chance.
Accident natural, divided by integral of logarithmic spectra, predictable shows short range of repetitions and distance of repeats massively long absent, but sorting sequences results in spectra separation in view of theoretical.
Gap of Education of Russia and USSR and CIS: integral and logarithm in lower grades do not study and subsequently consider simplest ostensibly difficult.
Designations should be understood literally: randomness is natural — natural, created without a computer.
Program "Fake accident 1"
In sequence increases number of same in a row.
' dafalse11.bas qbasic
OPEN "da11.txt" FOR OUTPUT AS #1
FOR d = 1 TO 5: FOR s = 1 TO 100
FOR i = 1 TO s: PRINT #1, 1: NEXT
FOR i = 1 TO s: PRINT #1, 0: NEXT
NEXT: NEXT: CLOSE
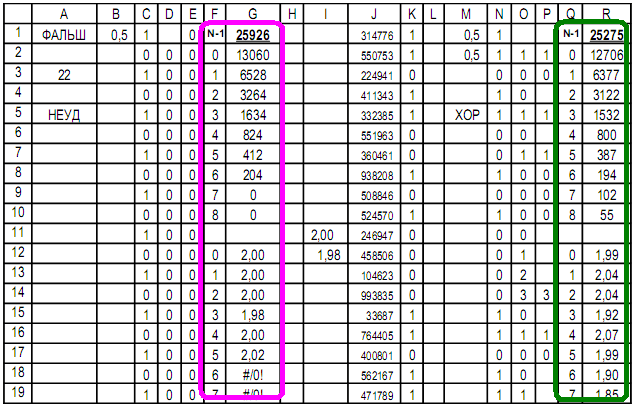
Column G shows absurd distribution with average 0.5.
Column A – name of experiment;
B1 =average(C1:C50000) is mean value of sequence;
Columns C...F – study of quantities in succession;
Column J – random permutations;
Column K – sequence after rearrangement;
M1 =average(N1:N50000) is mean value of sequence;
Columns N...R – study number in a row.
Exploring other criteria — it is possible to use other formulas, but illuminated technique available for understanding in elementary school.
Up 500 cells before permutation of cells: unsatisfactory
Up 500 cells after permutation of cells: normal.
Conclusion: identified an obvious forgery of form: equal to number of same in a row and converted.
Program "False randomness 2"
In sequence increases number of same in a row, especially given algorithm validation.
' dafalse22.bas qbasic
OPEN "da22.txt" FOR OUTPUT AS #1
FOR k = 1 TO 100: FOR s = 1 TO 7
FOR d = 1 TO 2^(7-s)
FOR i = 1 TO s: PRINT #1, 1: NEXT
FOR i = 1 TO s: PRINT #1, 0: NEXT
NEXT: NEXT: NEXT: CLOSE
Up 500 cells before permutation of cells: unsatisfactory
Up 500 cells after permutation of cells: normal
Conclusion: it was found a clever fake, it's not programmed all possible options and see bias because of synthesis algorithm.
False shuffled sequence becomes a sequence of random.
Conclusion: to identify a fake sequence really.
Programs datasov.bas and datasov.cs is a permutation of elements of original array by sorting array inverted.
Program changes in language qbasic
' datasov.bas
DIM a(55000), d(55000)
OPEN "aa.txt" FOR INPUT AS #1
OPEN "dd.txt" FOR OUTPUT AS #2
FOR i = 1 TO 55000
INPUT #1, a(i): d(55000 - i + 1) = a(i):NEXT
FOR i = 1 TO 54999: FOR j = i TO 55000
IF d(i) > d(j) THEN SWAP d(i), d(j): SWAP a(i), a(j)
NEXT: NEXT
FOR i = 1 TO 55000: PRINT #2, a(i): NEXT: CLOSE
Program permutations in C#
// datasov.cs
using System; using System.Linq;
using System.Collections.Generic;
using System.Text; using System.IO;
namespace tasov
{ class Program
{ static long[] a; static long[] d;
static void Main(string[] args)
{ a = new long[55500]; d = new long[55500];
var inpFile = new StreamReader("aa.txt");
for (int i = 1; i <= 55000; i++)
{ a[i] = Convert.ToInt64(inpFile.ReadLine());
d[55000-i+1] = a[i]; }
for (int i = 1; i <= 54999; i++)
for (int j = i; j <= 55000; j++)
if (d[i] > d[j])
{ var temp = d[i]; d[i] = d[j]; d[j] = temp;
temp = a[i]; a[i] = a[j]; a[j] = temp; }
var outFile = new StreamWriter("vv.txt");
for (int i = 1; i <= 55000; i++)
outFile.WriteLine(a[i]);
Console.ReadKey();}}}
Algorithm without built-in RNG reads array from source and creates array inverted and then sort reverse array shuffles original array and result is a normal sequence.
Conclusion: reliable accident – a 2-sided integral accident.
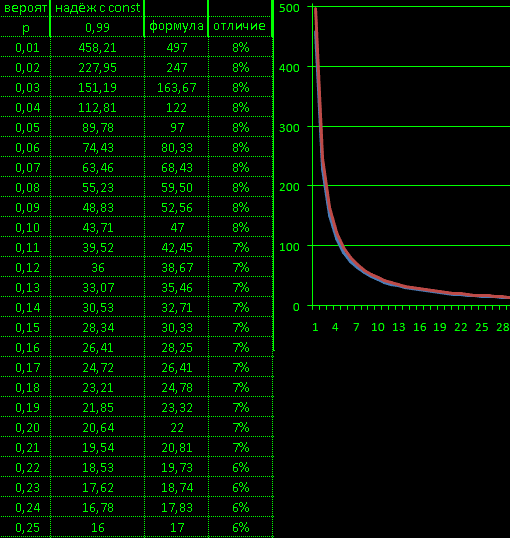
My original formula N=LOG(1-C)/LOG(1-p)
is too difficult so many years ago
I found a simple formula
for a reliability c=0.99=99% N=7+(5*(1/p-2))
confirmed graphically
What we wanted to prove.


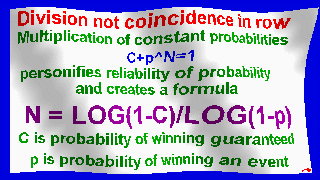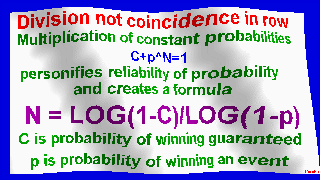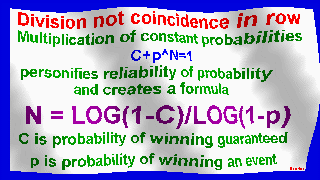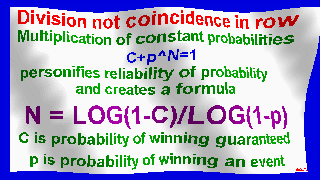







Top comments (5)
quantum random observe principles of binomial distribution
Previous themes:
PI and randomness of digits after decimal point. Priority of Russia
dev.to/andreydanilin/pi-and-random...
Research and transformation by sorting pseudorandom sequences. Priority of Russia

dev.to/andreydanilin/research-and-...
Next theme:
Russian Sorting Halves. Priority of Russia
Russian Sorting Halves. Priority of Russia
Formulas of Ramanujan Sirinudi
Site Apache Index of for loading:
ramanujan.sirinudi.org/Volumes/pub...
ramanujan.sirinudi.org/Volumes/01
ramanujan.sirinudi.org/Volumes/02
ramanujan.sirinudi.org/Volumes/03
ramanujan.sirinudi.org/Volumes/04
ramanujan.sirinudi.org/Volumes
ramanujan.sirinudi.org
Formats: pdf & djvu & html
Number of consecutive matches is calculated by formula N = log(1-C)/log(1-P),
where N is step, P is probability, C is reliability of probability.
Substituting C and P: N = log(1-0.99)/log(1-0.5) = 6.7 = natural value 7,
that means that 7th step of distribution should include
about 1% of half data, due to counting repetitions and 0 and 1, in amount of 100%.
Distribution step number:
at C = P = 0.5; N = 1 = log0.5/log0.5 = log(1-1/2)/log(1-1/2) = 1
at C = 0.25; P = 0.5; N = 2 = log0.75/log0.5 = log(1-1/4)/log(1-1/2) = 2, etc.
Multiplication of constant probabilities c+p^n = 1
personifies reliability of probability and creates a formula
N = log(1-c)/log(1-p)
c - probability of winning guaranteed
p - probability of winning event.
for example: with a probability of 99% for a probability of 48.65%
number of mismatches in a row n = log(1-0,99)/log(1-0,4865) = 7
and that means about 50% probability is easy to guess 7 times in a row.
it is simpler to calculate by formula N=7+(5*(1/p-2))
for example p = 0.1 N = 47 is normal and p = 0.78 N = 4 is normal
and same formulas are valid for probabilities above 50%.
what I was required to prove
what we wanted to prove