PI and randomness of digits after decimal point. Priority of Russia

PI and randomness of digits after decimal point. Priority of Russia

On March 14, on day "3.14", PI celebrates its day

Importance of topic: research on distribution of PI digits and irrational numbers opens up possibility of studying continuous data in real time,
when incoming data is counted without pauses for a separate input of data array

Understanding patterns of distributions human and natural and fake and machine actually apply results of 4 types of research:

1. Creation of randomness
2. Overcoming randomness
3. Falsification of randomness
4. Overcoming falsification of randomness

Gap of Education in Russia and CIS and USSR:
we don't study logarithm and integral in lower grades
and later consider simplest allegedly difficult
as well as algorithms for fast calculations are not studied

In addition fast computing algorithms are not taught in school,
although algorithms are clear in many programming languages
without use of quantum computers

But this work highlights public pyramid
spectral integral logarithmic binomial criterion

Using 55,000 digits of PI after decimal point,
first in a Word compatible program replace special characters
numbers are translated into a column and then in an Excel compatible
program digits are divided into binary attributes:
small \ large and even \ odd

Results: average for both binary distributions: about 0.5
and binary divisions correspond to theoretical probability

Table is applied:

Where are main formulas:
Cell-Formula-Explanation

C1 =AVERAGE(D1:D55000)
Average value of sequence numbers

C2 =AVERAGE(B1:B55000)
Average distribution value 1

D1 =IF(B1<C$2;0;1)
If number is less than average, then 0, otherwise 1

D2 =IF(B2<C$2;0;1)
If number is less than 1, then 0, otherwise 1, and so on.

E2 =IF(D2=D1;E1+1;0)
If distribution features are same, then counter of same attributes is +1,
otherwise counter is reset to zero

F2 =IF(E3=0;E2;" ")
If counter is reset to zero, largest counter is fixed

H2 =COUNTIF(F$1:F$55000;G2)
Number of signs 1 in a row and so on

H12 =H2/H3
Ratio of nearest number of attributes

J1 =IF(B1/2=ROUND(B1/2);0;1)
If number is even, then 0, otherwise 1

J2 =IF(B2/2=ROUND(B2/2);0;1)
If number is even, then 0, otherwise 1, etc

K2 =IF(J2=J1;K1+1;0)
If distribution features are same, then counter of same attributes is +1,
otherwise counter is reset to zero

L2 =IF(K3=0;K2;" ")
If counter is reset to zero, largest counter is fixed

N2 =COUNTIF(L$1:L$55000;M2)
Number of signs 1 in a row and so on

N12 =H2/H3
Ratio of nearest number of attributes

Other control functions can be programmed in table
You can create graphs of values of any cells in table

Continuation of table explores random permutations of sequence

Column Q - for a random permutation of integers up to 10^6,
to avoid repeating random events;
Column R - initially a copy of column B, later modified;
Columns T...AE - same as C...N columns"

Cell-Formula-Explanation

Q1 =RANDBETWEEN(0;1000000)
For a random permutation

Q2 =RANDBETWEEN(0;1000000)
Random for permutation, etc.

Preliminary conclusions: predominance of spectrum of repetitive features is found, what is typical for natural sequences, for example, by typing manually 3000 digits, 1st spectrum of repeated features will be higher than theoretical value

Using capabilities table for a permutation of elements of sequence and shuffled, spectra take on theoretical values as would be synthesized by RNG and CSPRNG and CPRNG

Spectra follow formula of Danilin: N = LOG(1-c)/LOG(1-p) by principle:
when C=P=0.5; N = 1 = log0.5/log0.5 = log(1-1/2)/log(1-1/2) = 1
for C=0.25; P=0.5; N = 2 = log0.75/log0.5 = log(1-1/4)/log(1-1/2) = 2, etc

Program for distribution spectra of random number
of consecutive identical features less \ more and even \ odd

Practical distributions correspond to theoretical ones
so random sequence is qualitative
and it is possible to study patterns of different sequences

Binomial Logarithmic Integral Pyramidal Distribution
BLIP distribution of Random numbers

'dablip.bas

RANDOMIZE TIMER
tb = TIMER: s = 0
OPEN "dablip.txt" FOR OUTPUT AS #2
n = VAL(MID$(TIME$, 7, 2))*10 ^ 5
DIM b(n), d(n), e(n), f(n)
DIM j(n), k(n), m(n), p(16), q(16)
LOCATE 1, 1: PRINT " THEORY Average BIG EVEN "

FOR i = 2 TO n-1
 b(i) = INT(RND*900)+100: s = s+b(i): m = s/i

 IF b(i) < m THEN d(i) = 0 ELSE d(i) = 1
 IF (b(i) MOD 2) = 0 THEN j(i) = 0 ELSE j(i) = 1

 IF d(i) = d(i-1) THEN e(i) = e(i-1)+1 ELSE e(i) = 0
 IF e(i) = 0 THEN f(i) = e(i-1) ELSE f(i) = 12
 IF f(i) > 12 THEN f(i) = 12

 IF j(i) = j(i-1) THEN k(i) = k(i-1)+1 ELSE k(i) = 0
 IF k(i) = 0 THEN m(i) = k(i-1) ELSE m(i) = 12
 IF m(i) > 12 THEN m(i) = 12

 p(f(i)) = p(f(i))+1: q(m(i)) = q(m(i))+1

 IF (i MOD 1000) = 0 THEN LOCATE 3, 1: PRINT i, " from ", n, INT(100*i/n); " %",
NEXT

LOCATE 3, 1: FOR t = 1 TO 12
 PRINT INT(n/(2^(t+1))), INT((p(t-1)+q(t-1))/2), p(t-1), q(t-1)
NEXT

te = TIMER
PRINT: PRINT te-tb; "second", INT(n/(te-tb)); " in second "
PRINT n, " elements ",

PRINT #2, te-tb; "second", INT(n/(te-tb)); " in second "
PRINT #2, n, " elements ",: PRINT #2,

PRINT #2,: PRINT #2, " THEORY Average BIG EVEN ": PRINT #2,
FOR t = 1 TO 12
 PRINT #2, INT(n/(2^(t+1))), INT((p(t-1)+q(t-1))/2), p(t-1), q(t-1)
NEXT

Feature of program: index of indixes p(f(i)) & q(m(i))

Results:

40 second 139'555 in second
5'600'000 elements

THEORY  Average BIG     EVEN

1400000 1400610 1399595 1401625
700000  700026  700122  699931
350000  349716  349508  349925
175000  174823  174892  174755
87500   87424   87564   87285
43750   43837   43931   43744
21875   22028   21983   22074
10937   10850   10865   10835
5468    5481    5496    5466
2734    2755    2732    2778
1367    1388    1396    1380
687     687     687     687

I think random have problems with parity:
parity of random changes too sharply

For self-study:

1. Uniformity of each of digits of PI
2. Methods for approximate calculation of PI
3. Learn 8 digits of PI after decimal point
4. Find formulas for calculating digits of PI
5. Remember circle length formulas

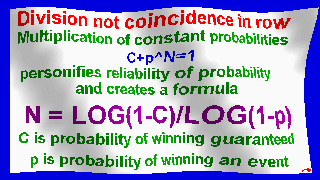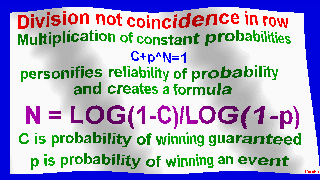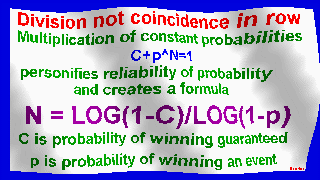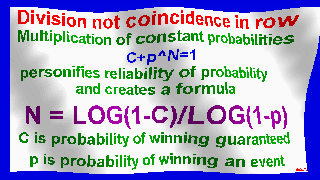
Comments

[AndreyDanilin]

Articles can be published:

1. Research and transformation by sorting of pseudo random sequences
2. Falsification of randomness and transformation by sorting pseudo random sequences

Target: to prove possibility of falsifying randomness and reality of overcoming falsification of randomness

[AndreyDanilin]

Russian Sortinging Halves Danilin visualisation

sorting fast and human
all on the topic: probability and reliability

!

[AndreyDanilin]

who allegedly doesn't understand: place 3000 digits typed manually
both my table and program will show a deviation from uniformity
so numbers were pressed by animate beings

Russian Sortinging Halves Danilin

[AndreyDanilin]

Next theme:
Research and transformation by sorting pseudo-random sequences. Priority of Russia
dev.to/andreydanilin/research-and-...