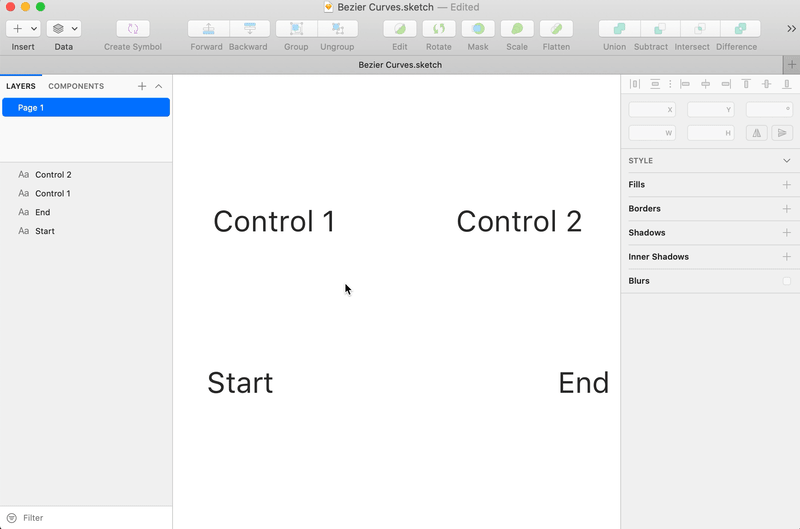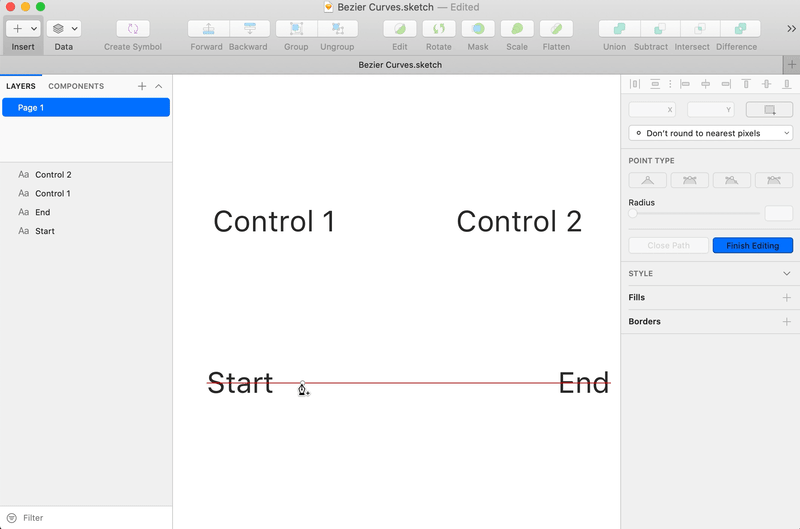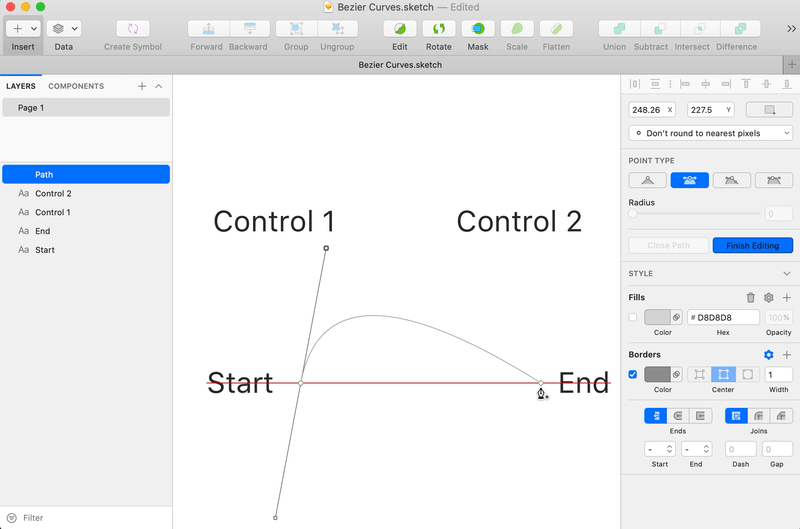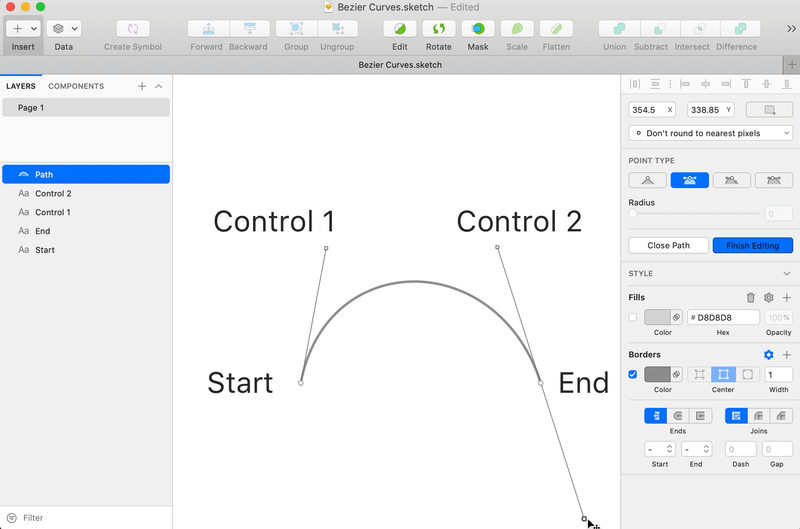
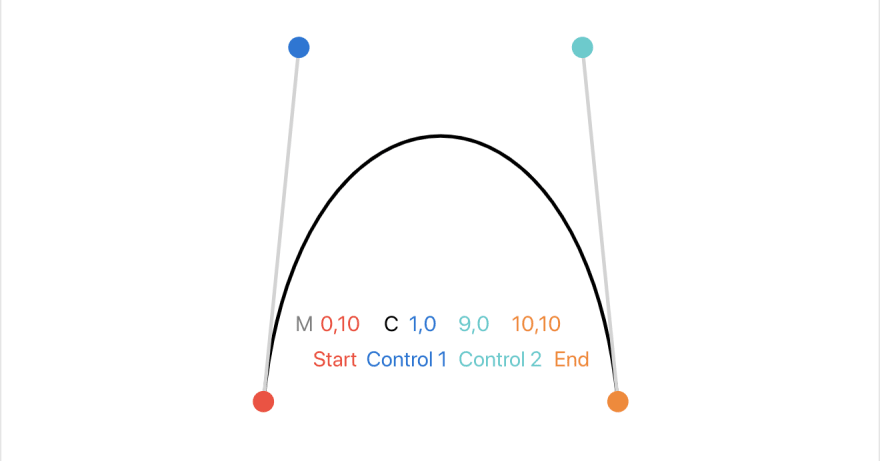
Bézier Curves are one of the 3 command types (with lines and arcs) of an SVG path. It is the mathematical name for a special type of curves that can be defined with 4 points: the "Start" point, the "End" point, and 2 "Control" points.
Most design tools allow you to draw Bézier curves (sometimes called "Pen tool" as in Photoshop, Illustrator, or Figma - or "Vector tool" as in Sketch) and let you define those 4 points.
The curve goes from the "Start" point to the "End" point while the "Control" points define its curvature.
The reason why those curves are so popular is because of how "smooth" they look like and how fast and easy they are to compute. You might even have done some curve stitching and already drawn one by hand in the case where the 2 control points are the same (this is a special case of Bézier Curves but we will come back to it later).
How does it work?
To get a feel of how Bézier Curves work, imagine you are building a segment of a railway track between 2 places 🚂. The direction and the speed of the train at the beginning and the end are a constraint given by the railway controllers in order for the traffic to be good across the line.
Between the 2 places, the journey needs to be as smooth as possible, which means that the track needs to turn the least possible while respecting the instructions of the controllers.
In our case, that means continuing in the same direction as we arrive while slowly turning to the right.
If there was no speed constraint at the end (and so no direction), we could turn until we face the end and then go straight towards it. Otherwise, we need to take some leeway to match the direction at the end.
How does it translate to SVG?
The Curve command
The command associated with a Bézier Curve is C. The start point is always a given (the position at the end of the previous command - or (0,0) if it's the first command).
The Smooth Curve command
There are also some special cases of Bézier Curves that have shortcut notations in SVG.
A common case is when you have multiple curves one after the other and you want it to smoothly transition between them. To do so, you need to have the first control point of the next curve be the reflection of the second control point of the previous curve. So as long as you specify one, you shouldn't need to specify the other one. That's what the S command is for (S for smooth).
If you look back at the Sketch screencast, you will notice that we actually define the reflection of the second control point, implicitly preparing for the next curve segment.
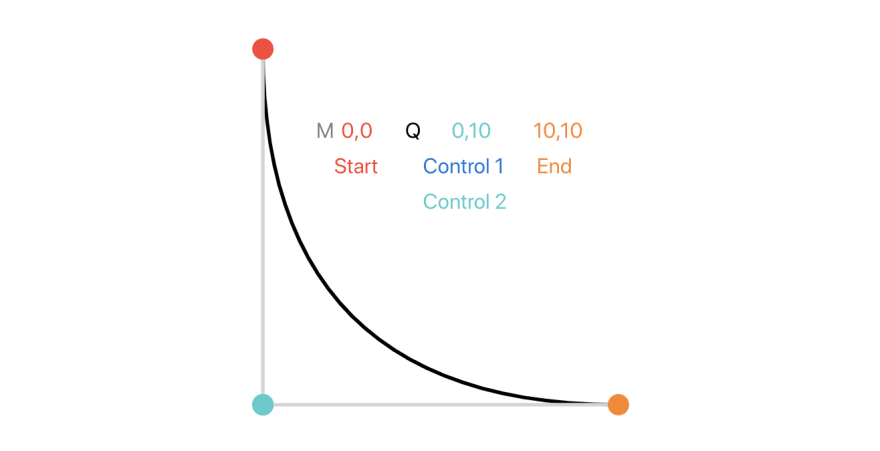
The Quadratic Curve command
Another case is when both control points are superimposed. In that case, you also don't need to specify them both, only one is enough. That what the Q command is for (Q for quadratic).
That's our curve stitching drawing!
The Smooth Quadratic Curve command
Now, what if we want to continue our quadratic Bézier Curve with another quadratic Bézier Curve? Well, we only have to specify the end point! That what the T command is for (T for Smooth Quadratic obviously).
This explanation is taken from SVG Path Visualizer, a tool to visualize and explain how SVG paths work.








Top comments (0)