My notes on Linked list with an implementation in Java.
You can find the complete code for this and other data structures here: data structures and algorithms
A linked list is a data structure that uses nodes that hold both a value and a reference to the next node.
Common Operations for a linked list includes:
| Operation | Complexity |
|---|---|
| get(indexOfElement) | O(n) |
| insert(index, value) | O(n) |
| find(value) | O(n) |
| delete(value) | O(n) |
This is the node we will be using:
public class SingleNode<T extends Comparable<? super T>>{
private T value;
private SingleNode<T> nextNode;
In this implementation of the linked list we will hold both a reference to the head and the tail of the list. We will be only accepting objects of classes that implement the Comparable interface since that way we can easily compare between two values.
public class LinkedList<T extends Comparable<? super T>> {
private int size;
private SingleNode<T> head;
private SingleNode<T> tail;
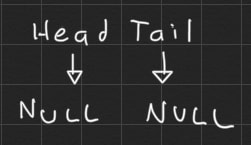
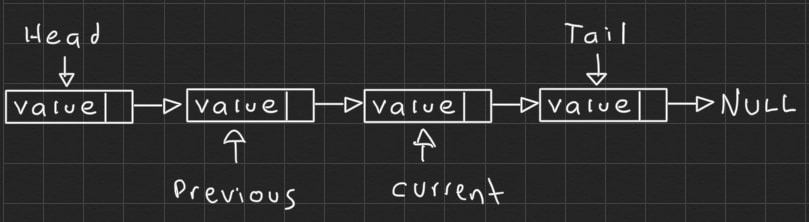
At the beginning the list will look like this:
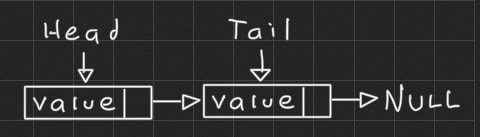
If we add an element to the list it will look like this, with both head and tail pointing to the same node.
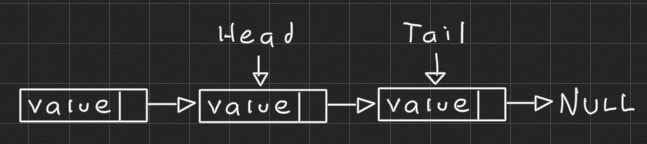
To append an element at the end of the list we can use the tail reference, add the element as the next element of the tail:
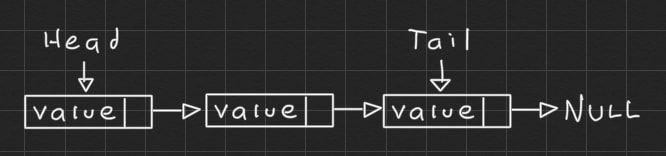
Then we update the tail reference:
public void add(T value) {
if(size == 0) {
head = new SingleNode<T>(value, null);
tail = head;
} else {
tail.setNextNode(new SingleNode<T>(value, null));
tail = tail.getNextNode();
}
size++;
}
For prepending an element to the beginning of the list we first create the new element and set the head as the new elements next node:
And then we update the head reference
public void prepend(T value) {
if(size == 0) {
head = new SingleNode<T>(value, null);
tail = head;
} else {
head = new SingleNode<T>(value, head);
}
size++;
}
To find a value from an index we just iterate the linked list counting every node.
private SingleNode<T> getSingleNodeByIndex(int index) {
if(size <= 0 || index >= size) {
throw new IndexOutOfBoundsException();
}
if(index == 0) {
return head;
}
if(index == size - 1 ) {
return tail;
}
SingleNode<T> singleNode = head.getNextNode();
for(int i = 1; i < index; i++) {
singleNode = singleNode.getNextNode();
}
return singleNode;
}
To find the index of an element using the value we just iterate the linked list until we run out of list, or we find the element.
public int indexOf(T value) {
SingleNode<T> singleNode = head;
for(int i = 0; i < size; i++) {
if (singleNode.getValue().compareTo(value) == 0) {
return i;
} else {
singleNode = singleNode.getNextNode();
}
}
return -1;
}
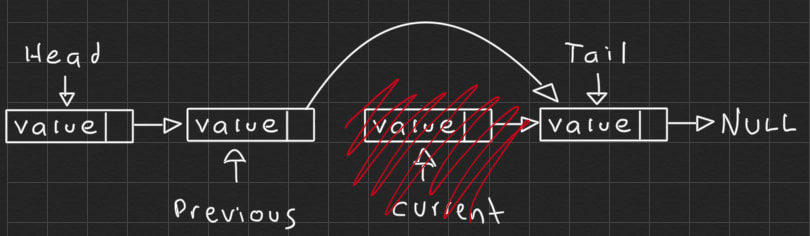
To remove an element using its value we will use two references, previous and current, and when current points to the value we want to remove we will use the previous reference to take out of the list the element we want to remove.
Suppose in this case current points to the value we want to remove:
We update the next node of previous:
public void removeByValue(T value) {
if(size == 0) {
return;
}
SingleNode<T> beforeValue = null;
SingleNode<T> valueToCompare = head;
for(int i = 0; i < size; i++) {
if (valueToCompare.getValue().compareTo(value) == 0) {
if(i == 0) {
head = head.getNextNode();
} else {
beforeValue.setNextNode(valueToCompare.getNextNode());
if (i == size - 1) {
tail = beforeValue;
}
}
size--;
break;
} else {
beforeValue = valueToCompare;
valueToCompare = valueToCompare.getNextNode();
}
}
}
Insertion at any index works by getting a reference to the node right before the index where we want to insert, and then updating the next node references.
public void add(T value, int index) {
if(size <= 0 || index >= size) {
throw new IndexOutOfBoundsException();
}
if(index == 0){
prepend(value);
} else if (index == size - 1) {
add(value);
} else {
SingleNode<T> beforeNewNode = getSingleNodeByIndex(index - 1);
beforeNewNode.setNextNode(new SingleNode<T>(value, beforeNewNode.getNextNode()));
size++;
}
}
Download the complete code for this and other data structures here: data structures and algorithms






Top comments (0)