Authors:Michal Harcej, 22 Dec, michalharcej@gmail.com
Abstract:
The traditional mass-energy equivalence principle, encapsulated by Einstein’s equation (E=mc^2), provides a static relationship between mass and energy. However, in observer-rich systems—such as those encountered in quantum mechanics, economics, and blockchain technology—mass is not merely a function of energy but also of coherent observation and narrative validation. This paper introduces the Tau Transform, a novel mathematical operator that extends the concept of mass-energy equivalence by embedding witnessing and coherence into the fabric of transmutation. We define the Tau Transform as:
**[M = \frac{1}{c^2} \int_{-\infty}^{\infty} E(t) \cdot \kappa(t) \, dt]
where (M) is the emergent mass, (E(t)) is the energy density field, and (\kappa(t)) is the coherence kernel encoding attention, phase alignment, and narrative validity. We formalize (\kappa(t)) as a computable operator, derive the Attention Cost of value stabilization, and demonstrate applications in quantum-symbolic reasoning, economic forecasting, and integrity-aware blockchain systems. Our framework redefines energy not as the ultimate commodity but as raw potential, while coherent attention becomes the true mint of reality.
1. Introduction
Einstein’s mass-energy equivalence, (E=mc^2), revolutionized our understanding of the physical world by establishing a direct relationship between mass and energy. However, this equation, while profound, does not account for the role of observation and coherence in the transformation of energy into mass. In systems where data is abundant, quantum superpositions are prevalent, and narratives compete, the emergence of mass is a dynamic process influenced by the act of witnessing and the coherence of that witnessing.
This paper addresses the incompleteness of (E=mc^2) in observer-rich systems by introducing the Tau Transform, a framework that incorporates the role of attention and coherence in the transformation of energy into mass. We propose a new equation:
[M = \frac{1}{c^2} \int_{-\infty}^{\infty} E(t) \cdot \kappa(t) \, dt]
where (\kappa(t)) is a coherence kernel that captures the essence of attention, phase alignment, and narrative validity. This framework has implications for various fields, including quantum mechanics, economics, and blockchain technology, where the emergence of value and meaning is governed by coherent observation.
2. The Tau Transform: Formal Definition
2.1 Emergent Mass and Energy Density Field
The emergent mass (M) is defined as the integral of the energy density field (E(t)) weighted by the coherence kernel (\kappa(t)):

[M = \frac{1}{c^2} \int_{-\infty}^{\infty} E(t) \cdot \kappa(t) \, dt]
Here, (E(t)) represents the raw potential energy at time (t), and (c) is the speed of light, preserving relativistic invariance.
2.2 Coherence Kernel (\kappa(t))
The coherence kernel (\kappa(t)) is a normalized witness function that encodes attention, phase alignment, and narrative validity. It is defined as:

[\kappa(t) = \frac{1}{Z} \int_{-\infty}^{t} N(t') \cdot C[\psi(t')] \cdot e^{-\lambda (t - t')} \, dt']
where:
- (N(t')) represents narrative priors at time (t'), capturing the density or weight of symbolic knowledge or archetypes active at that time.
- (C[\psi(t')]) is the coherence functional, quantifying how well the current system state matches symbolic or archetypal structures.
- (\lambda) is the decay constant, representing symbolic forgetfulness or entropy growth.
- (Z) is the normalization constant, ensuring that (\int \kappa(t) \, dt = 1).
2.3 Narrative Priors (N(t))
The narrative priors (N(t)) are defined as:
[N(t) = \sum_{i=1}^{k} w_i \cdot \delta(\psi_i, \psi(t))]
where:
- (\psi_i) are archetypal states (e.g., "Hero rises", "Fall of Tower", "Union of Opposites").
- (w_i) are weights from a narrative knowledge base, trained on mythology, news, and memetic traces.
- (\delta(\psi_i, \psi(t))) is a symbolic similarity function, such as cosine similarity of embeddings.
2.4 Coherence Functional (C[\psi])
The coherence functional (C[\psi]) is defined as:

[C[\psi] = 1 - \frac{H(\psi)}{H_{\text{max}}}]
where:
- (H(\psi)) is the narrative entropy, representing the Shannon entropy over symbolic states or meanings.
- (H_{\text{max}}) is the maximum entropy for the symbolic state space.
2.5 Attention Cost (C_{\text{focus}})
The attention cost (C_{\text{focus}}) is defined as the ratio of total system attention spent to the effective symbolic throughput:
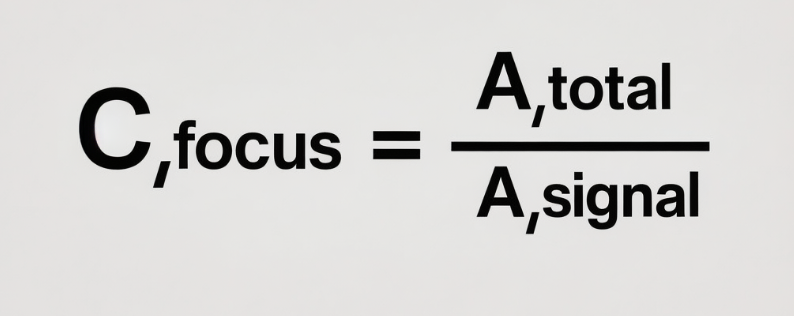
*[C_{\text{focus}} = \frac{A_{\text{total}}}{A_{\text{signal}}}]
*
where:
- (A_{\text{total}}) is the total system attention spent (e.g., hashpower, validator time, user participation).
- (A_{\text{signal}}) is the effective symbolic throughput, representing how much of the effort moves the system toward the intended state.
3. Methods
3.1 Mathematical Formulation
We derive the mathematical formulation of the Tau Transform, including the coherence kernel (\kappa(t)) and the attention cost (C_{\text{focus}}). We provide detailed derivations and proofs to ensure the mathematical rigor of our framework.
3.2 Computational Implementation
We discuss the computational implementation of the Tau Transform, including algorithms for calculating the coherence kernel (\kappa(t)) and the attention cost (C_{\text{focus}}). We provide pseudocode and examples to illustrate the practical application of our framework.
4. Results
4.1 Quantum-Symbolic Reasoning
We demonstrate the application of the Tau Transform in quantum-symbolic reasoning. We show how the coherence kernel (\kappa(t)) can be used to model the emergence of mass in quantum systems, where observation and coherence play a crucial role.
4.2 Economic Forecasting
We apply the Tau Transform to economic forecasting, showing how the coherence kernel (\kappa(t)) can be used to model the emergence of value in economic systems. We provide examples of how the attention cost (C_{\text{focus}}) can be used to predict market trends and stabilize value.
4.3 Blockchain Systems
We demonstrate the application of the Tau Transform in blockchain systems, showing how the coherence kernel (\kappa(t)) can be used to model the emergence of value and integrity in blockchain transactions. We provide examples of how the attention cost (C_{\text{focus}}) can be used to enhance the efficiency and security of blockchain consensus mechanisms.
5. Discussion
5.1 Implications for Physics
The Tau Transform provides a new perspective on mass-energy equivalence, incorporating the role of observation and coherence in the transformation of energy into mass. This framework has implications for our understanding of quantum mechanics, thermodynamics, and the nature of reality.
5.2 Implications for Economics
The Tau Transform provides a new framework for understanding the emergence of value in economic systems. By incorporating the role of attention and coherence, this framework can help predict market trends, stabilize value, and enhance the efficiency of economic systems.
5.3 Implications for Blockchain Technology
The Tau Transform provides a new framework for understanding the emergence of value and integrity in blockchain systems. By incorporating the role of attention and coherence, this framework can help enhance the efficiency and security of blockchain consensus mechanisms.
6. Conclusion
The Tau Transform is a novel framework that extends the concept of mass-energy equivalence by incorporating the role of observation and coherence in the transformation of energy into mass. This framework has implications for various fields, including quantum mechanics, economics, and blockchain technology. By redefining energy as raw potential and coherent attention as the true mint of reality, the Tau Transform provides a new perspective on the emergence of value and meaning in observer-rich systems.
7. References
[1] Einstein, A. (1905).
**Copyright©2025





Top comments (0)