Building Binary Search Trees with JavaScript

What are Binary Search Trees?

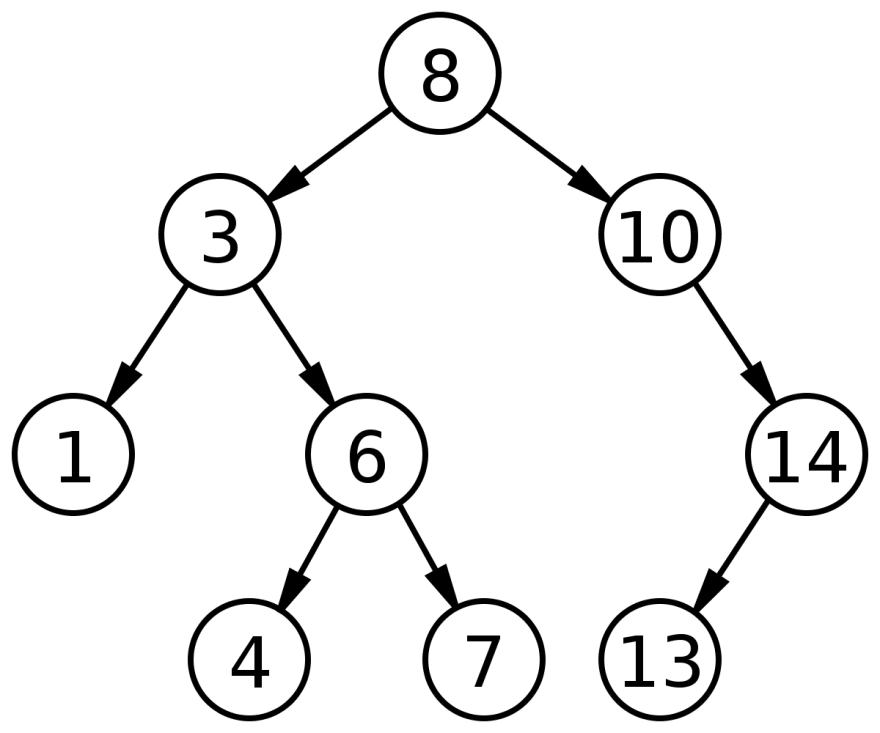
Binary Search Trees are a node-based data structure that we use in computer science to organize data. Each node can have up to two children nodes.

As we add nodes to our tree, there are only two places that node can go: to the left or the right of the root or parent node. If the value of the incoming node is less than the parent node, it will go to the left. If the value of the incoming node is greater than the parent node, it will go to the right.

In general, all Binary Search Trees are built with three methods:

1. Insert - which adds a value to our tree
2. Contains - which checks if a value is present in our tree
3. depthFirstLog - which takes a function and calls that function and executes it on each value within the tree

Today we'll build our own Binary Search Tree with JavaScript objects that include all three methods above as functions. But first, we need to create our node constructor function.

Build our BST node constructor

Since a BST is made up of nodes, we need to create a node constructor function. Just to bring a little life to this example, I'm going to create a BST that will take in a few players from my hometown Atlanta Hawks and compare their Player Efficiency Rating to the league average PER of 15.

const BinarySearchTree = function(playerObj) {
  // creating a node that will be an object
  let node = Object.create(BinarySearchTree.prototype)
  // creating a name property that takes the name of the player and assigns it to the node
  node.name = playerObj.name
  // creating a value property that takes the PER of the player and assigns it to the node
  node.value = playerObj.per
  // creating a left and right property that are undefinded
  node.left = undefined;
  node.right = undefined;

  return node;
};

Now this code is ready to take our first "player" object the league average parent node that has a PER of 15.

const leagueAvg = {
  name: "League Avg",
  per: 15.00
};

const hawksBST = BinarySearchTree(leagueAvg);

So when we call our BinarySearchTree function with our leagueAvg "player", we can now start adding our other player objects. But first, we need to build our Insert Method.

Building our Insert Method

The first step of our insert method is checking if the input value is greater than or equal to the root node. If it's less than, we check the left node to first see if it even exists. If it doesn't, great! We simply turn that playerObj into a node and put it to the left of our root node.

If there is a node already there, we can use recursion to the same evaluation, only this time instead of referring to the parent node at the top of the tree, we're referring to the child node.

BinarySearchTree.prototype.insert = function(playerObj) {
// checking if the input per is less than the node's value
  if(playerObj.per < this.value) {
  // if true, check if the left property is undefined
    if(!this.left) {
    // if true, create a new node with the playerObj
      this.left = new BinarySearchTree(playerObj);
    // if false, call insert on that playerObj 
    } else {
      this.left.insert(playerObj)
    }
// now checking if the input per is greater than the node's value
  // the rest of the logic is similar to the left's above
  } else if (playerObj.per > this.value) {
    if(!this.right) {
      this.right = new BinarySearchTree(playerObj)
    } else {
      this.right.insert(playerObj);
    }
  }
}

As you'll notice, we use the same exact logic for the right side as well if the input player object has a higher PER than league average.

To see if this works, let's add some objects.

const playerObjs = [{
  name: "Trae Young",
  per: 23.9
},
{
  name: "John Collins",
  per: 23.5
},
{
  name: "Kevin Huerter",
  per: 11.5
},
{
  name: "Deandre Hunter",
  per: 8.6
},
{
  name: "Cam Reddish",
  per: 9.0
}]

After we run our loop over the playerObjs array, we can see that all objects have been turned into nodes within our Binary Search Tree.

// calling insert on each object within our collection
playerObjs.forEach(obj => hawksBST.insert(obj))

BinarySearchTree {
  name: 'League Avg',
  value: 15,
  left: BinarySearchTree {
    name: 'Kevin Huerter',
    value: 11.5,
    left: BinarySearchTree {
      name: 'Deandre Hunter',
      value: 8.6,
      left: undefined,
      right: [BinarySearchTree]
    },
    right: undefined
  },
  right: BinarySearchTree {
    name: 'Trae Young',
    value: 23.9,
    left: BinarySearchTree {
      name: 'John Collins',
      value: 23.5,
      left: undefined,
      right: undefined
    },
    right: undefined
  }
}

Building our Contains Method

Contains is used on a BST to determine if an input value exists as a node within the tree. Like our insert method, we'll start at the top, then work our way down, starting at the left if the input value is less and starting at the right if it's greater. We'll also check if the the right and left nodes are actually defined.

Again, since we've already built our basic contains at the beginning of our function, we can use recursion to call that function again on each node.

BinarySearchTree.prototype.contains = function(playerObj) {
// checking if the value of the parent node is equal to the input value
  if(this.value === playerObj.per) {
    return true;
// now checking if the left node contains the value
  } else if(this.value > playerObj.per && this.left !== undefined) {
    return this.left.contains(playerObj)
// now checking if the right node contains the value
  } else if(this.value < playerObj.per && this.right !== undefined) {
    return this.right.contains(playerObj)
  }
  return false;
}

Building our depthFirstLog Method

depthFirstLog allows us to run a callback function over each node in the tree. So let's make a callback. I actually forgot to include the team name for each node, so let's build a callback that goes through each node and add's a teamName property and gives it a value of "Atlanta Hawks".

cost addTeamName = node => {
  if(node.name !== "League Avg") {
    node.team = "Atlanta Hawks"
  }
}

BinarySearchTree.prototype.depthFirstLog = function(callback) {
  //invoke callback function on this.value
  callback(this);
  //if this.left doesn't exist
  if (this.left) {
    //recursively call .depthFirstLog on this.left & callback
    this.left.depthFirstLog(callback);
  }
  //if this.right doesn't exist
  if (this.right) {
    //recursively call .depthFirstLog on this.right & callback
    this.right.depthFirstLog(callback);
  }
};

hawksBST.depthFirstLog(addTeamName);

You'll notice our callback has one condition: if the name value is not strictly equal to "League Average", we'll update the node. We're only doing this because we don't want our root node to have a team name.

Just like the other methods, we can use recursion to invoke our callback over each node.

BinarySearchTree {
  name: 'League Avg',
  value: 15,
  left: BinarySearchTree {
    name: 'Kevin Huerter',
    value: 11.5,
    left: BinarySearchTree {
      name: 'Deandre Hunter',
      value: 8.6,
      left: undefined,
      right: [BinarySearchTree],
      team: 'Atlanta Hawks'
    },
    right: undefined,
    team: 'Atlanta Hawks'
  },
  right: BinarySearchTree {
    name: 'Trae Young',
    value: 23.9,
    left: BinarySearchTree {
      name: 'John Collins',
      value: 23.5,
      left: undefined,
      right: undefined,
      team: 'Atlanta Hawks'
    },
    right: undefined,
    team: 'Atlanta Hawks'
  }
}

Conclusion

A great component of Binary Search Trees are, well, their binary nature.

After the we establish the root node, the only thing we need to evaluate is our input value relative to the parent node and potentially the the two child nodes after that.

This kind of structure generally delivers on a linear (O(n)) time complexity and, at worst case, a quadratic O(n^2) time complexity in algorithms if the tree is rather long or one-sided.

As you're learning more data structures, I highly recommend using real life data like PER to help your understanding.