This is what I think is the best way of explaining Applicative Functor.
The objective of this post is to give anyone, who is not neccessarily mathematically trained, the mathematical intuition behind Applicative Functor.
It all begins with the simplest possible mathematical structure called Apply.
What is Apply?
You may think that you are not familiar with it but trust me, you already are an expert. apply is a binary function that takes a function and a then apply to then return it.
Basically it’s the name for the notation f(x) that you have been using all the time in programming and mathematics. You probably didn’t even bother to learn it’s name because you have been taking it for granted.
Although it looks so trivial, it has rules, namely Applicative rules.
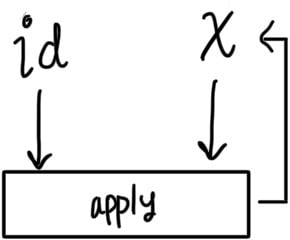
Rule 1 - identity
must always yield
itself where id is a function that returns the input as it is.
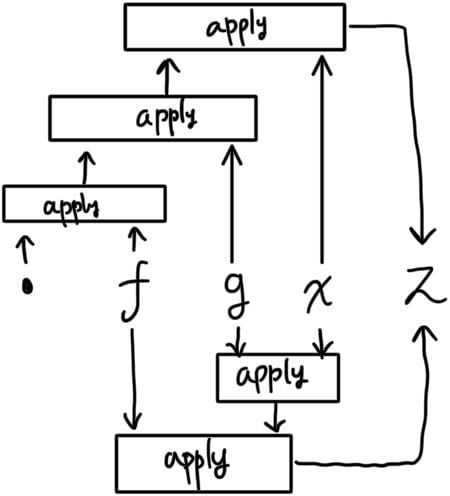
Rule 2 - composition
Follwing must hold
Note that results in a curried form of composition .
Those seemingly trivial rules keep mathematics and programming making sense.
So what is applicative functor?
Preserving mathematical structure is a fundamental concept of mathematics. You can find it everywhere. For example, matrix preserves linearity, homomorphism preserves algebraic structure, continuous function preserves topological structure, functor preserves Categorical structure etc.
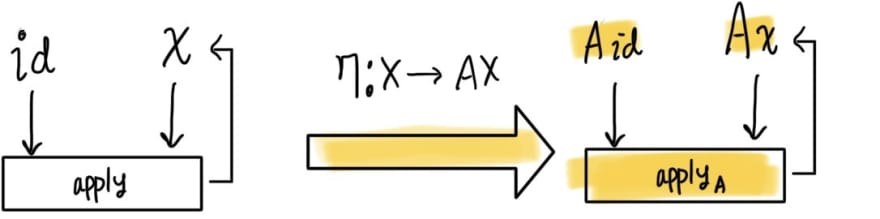
Applicative Functor preserves Applicative rules that we have just mentioned in addition to Categorical structure. In other words, Applicative functor will provide a universal construction(means it will work on any elements x of any type X) (call it
)
and which is the same as apply but for the types that are lifted by A.
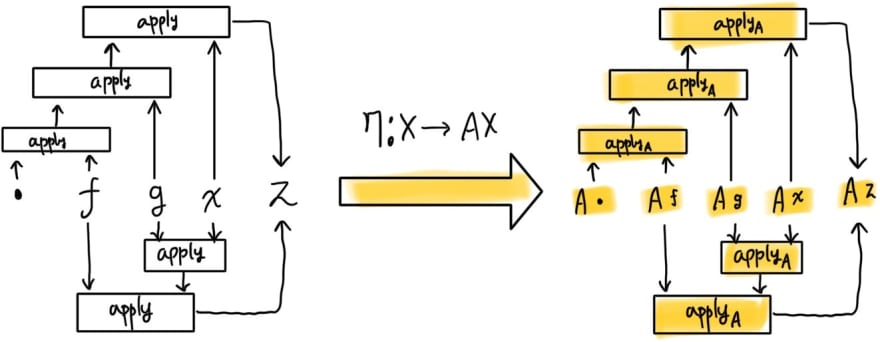
and any given two composable functions
and
and an element
from the function’s domain will preserve their applicative structure after they are transformed by
.
It’s all about preserving the structure.
Note that is widely known as pure or return to programmers, as ap.
Applicative Functor as “Functor for binary operators”
I know many people think Applicative Functor as “Functor for binary operators”. It’s because preserving Applicative rules gives rise to preserving binary operators, and it’s very practical and ubiquitous. Let’s see how it works.
In other words, lets see how given a binary operator
and an Applicative Functor
We can construct following new binary operator
And it preserves all the original operator’s structure, e.g associativity, identity, commutativity etc.
Thinking of why Functor alone can’t do the job can gives you lots of insight through it. If you try to juggle with Functor alone to achieve the construction, you will soon realise it’s impossible. The reason is that a function as an object pops up and Functor alone is too weak to apply an object to a function as an object. Because Functor can only apply an object to a function as a morphism.
Here’s the construction.
think of + as the curried form.
then
the new object’s type is
then apply it to the curried form of applyA
the new object’s type is
You can see it became a function
Since it’s a function now, compose it with .
the new function’s type is
Boom! construction is done.
Conclusion
Applicative functor is nothing but a preservation of one of the easiest mathematical structure apply. There’s nothing to overthink about it.



Top comments (0)