I've taken a little break from my sorting series in Ruby, but I'm back again!
This time with a sorting algorithm that really caught my eye, cycle sort.
Overview
First, a little overview about the cycle sort algorithm:
- Cycle sort is an in-place sorting algorithm
- Cycle sort's main attraction is it's ability to sort in-place and really attempts to optimize in terms of space
- Cycle sort is also an unstable sorting algorithm
- This essentially means that duplicate values in the array may appear in a different order after sorting than they did originally
Time Complexity
Cycle sort really isn't as concerned with time complexity as it is with space, which can be made clear from the chart below:
| Time | Case |
|---|---|
| O(n2) | average case run time |
| O(n2) | worst case run time |
| O(n2) | best case run time |
We can obviously see that cycle sort really isn't optimizing for time complexity here. Especially if we compare it to the sorting algorithms that we've gone over so far, this one seems to be quite slow.
Each value needs to be iterated over at least once, and if we have n values in the array, that easily becomes O(n2). It could be very ineffective on large lists.
But what cycle sort lacks in time saving it makes up for in space! By using comparisons it is theoretically very optimal in terms of how many changes it makes in memory. Worst case its space complexity is O(n).
Theory/Break Down
Now for the theory of the cycle sort algorithm. When I say theory I find it the most helpful to visualize what the actual process is and then we can code it up.
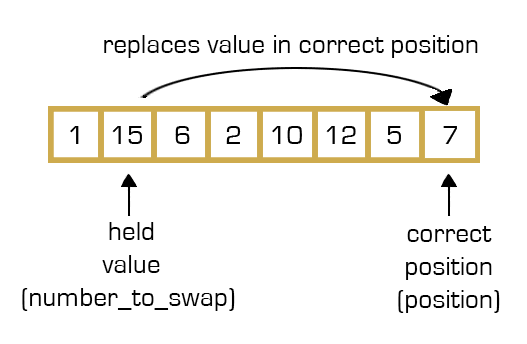
Cycle sort works by first taking the 0 index in the array, and storing that value temporarily. It then walks through the array to find where this held value belongs by comparing this value to all of the other elements in the array. By understanding which values are larger and smaller it can determine where it should place itself.
After placing itself, it swaps its own value with the value that was in its correct location. Now the new held value is the value that originally belonged to the position it determined it belonged in.
After that it moves along in the array, running this same procedure for all of the values until it reaches the end and the array is correctly sorted.
Actual Code
Alright, on to the part you've been probably waiting for, the code! This is just my implementation of cycle sort in Ruby and you can feel free to play with it and change it around to whatever works best for you.
def cycle_sort(array, swaps)
swaps = 0
cycle_start = 0
while cycle_start < array.length - 1
number_to_swap = array[cycle_start]
position = cycle_start
i = cycle_start + 1
while i < array.length
if array[i] < number_to_swap
position += 1
end
i += 1
end
if position != cycle_start
while number_to_swap == array[position]
position += 1
end
array[position], number_to_swap = number_to_swap, array[position]
swaps += 1
end
while position != cycle_start
position = cycle_start
j = cycle_start + 1
while j < array.length - 1
if array[j] < number_to_swap
position += 1
end
while number_to_swap == array[position]
position += 1
end
j += 1
end
array[position], number_to_swap = number_to_swap, array[position]
swaps += 1
end
cycle_start += 1
end
return array, swaps
end
print(cycle_sort([120, 20, 12, 1, 5, 5, 78], [0]))
This explanation is going to be a bit long, so get ready!
First we declare our two variables, swaps and cycle_start. Swaps is just for us to know at the end how many changes the array had to make for itself in memory to be sorted. And cycle_start is where we will begin iterating over our array.
Our main while loop goes from cycle_start to the length of the array minus 1. This is because we cannot compare a value to one that doesn't exist and we don't want to throw an error because of that.
Next we save our 0 index array value into our number_to_swap variable. This will be held until we can locate the position in which this value belongs. We then set our position value to be equal to our cycle_start value as we will start at the beginning to calculate where our value belongs.
Now we have our second while loop, this one is going to iterate from i to the length of the array, and i is declared as cycle_start plus 1. This is done to check each value in the array to see if it is smaller than the number_to_swap that we're holding on to. If there are any values smaller than our held number, we will increase the position variable. We can see here that by increasing our position variable we are essentially figuring out where our held value belongs by comparing our held value to all of the other values in the array.
The rest of the code pretty much depends on whether or not we have values smaller than the value we have held. If this is not the case, and our held value is the smallest, then we will skip all of the rest of the code, and increase our cycle_start to begin again. Essentially, we will not need to swap any values if our 0 index value is already the smallest and thusly sorted.
But, if there were smaller values than our number_to_swap, then we'll need to check for duplicates, and then swap the value held with the one in the position where it belongs.
After that is done, then we will go into a new while loop that essentially does the exact same thing as our previous while loop, setting the position to cycle_start and checking again if the new number_to_swap value we have is larger than any of the other elements in the array. It then continues this process that keeps swapping until the array is sorted.
This was a long one for sure, and the idea of cycle sorting is fairly complex in my opinion. So if you're like me, and would love a visual of how this works, check out the resources below:
Resources
I hope that this could be helpful for you and I'll catch you for the next installment of my sorting algorithm series! Happy coding 😊


Top comments (0)