LeetCode - Validate Binary Search Tree

Problem statement

Given the root of a binary tree, determine if it is a valid binary search tree (BST).

A valid BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees.

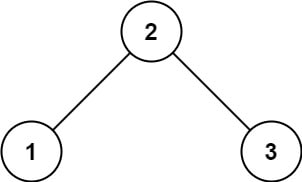
Example 1:

Input: root = [2, 1, 3]
Output: true

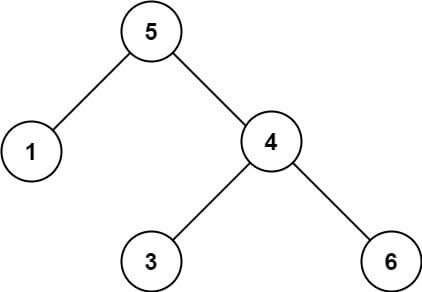
Example 2:

Input: root = [5, 1, 4, null, null, 3, 6]
Output: false
Explanation: The root node's value is 5, but its right child's value is 4.

Constraints

- The number of nodes in the tree is in the range [1, 10^4].
- -2^31 <= Node.val <= 2^31 - 1

Explanation

Incorrect approach

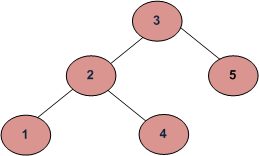
The first naive approach most of us will think of is to check
for every node, the left child should be the smaller and the right child should be greater.

But the below tree is not a valid BST as the node with value 4 is in the the left subtree of the node with value 3.

Correct approach

The above approach hints that we need to keep track of the maximum and minimum value for any node in its left and right subtree.

Let's check the algorithm.

// isValidBST function
- if root == NULL
  - return true

- return checkValidBST(root, LONG_MIN, LONG_MAX)

// checkValidBST(root, min, max) function
- if root == NULL
  - return true

- if root->val <= min || root->val >= max
  - return false

- return checkValidBST(root->left, min, root->val) && checkValidBST(root->right, root->val, max)

C++ solution

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        if(root == NULL) {
            return true;
        }

        return checkValidBST(root, LONG_MIN, LONG_MAX);
    }

    bool checkValidBST(TreeNode* root, long min, long max){
        if(root == NULL) {
            return true;
        }

        if(root->val <= min || root->val >= max) {
            return false;
        }

        return checkValidBST(root->left, min, root->val) && checkValidBST(root->right, root->val, max);
    }
};

Golang solution

func isValidBST(root *TreeNode) bool {
    if root == nil {
        return true
    }

    return checkValidBST(root, math.MinInt32, math.MaxInt32)
}

func checkValidBST(root *TreeNode, min, max int) bool {
    if root == nil {
        return true
    }

    if root.Val <= min || root.Val >= max {
        return false
    }

    return checkValidBST(root.Left, min, root.Val) && checkValidBST(root.Right, root.Val, max)
}

Javascript solution

var isValidBST = function(root) {
    if( !root ) {
        return true;
    }

    return checkValidBST(root);
};

var checkValidBST = function(root, min = -Infinity, max = +Infinity) {
    if (!root) {
        return true;
    }

    if (root.val <= min || root.val >= max) {
        return false;
    }

    return checkValidBST(root.left, min, root.val) && checkValidBST(root.right, root.val, max);
}

Let's dry-run our algorithm to see how the solution works.

Input: root = [2, 1, 3]

// in isValidBST function
Step 1: if root == NULL
           false

Step 2: return checkValidBST(root, LONG_MIN, LONG_MAX)

// in checkValidBST function
Step 3: if root == NULL
           false

Step 4: if root->val <= min || root->val >= max
           2 <= LONG_MIN || 2 >= LONG_MAX
           false || false
           false

Step 5: return checkValidBST(root->left, min, root->val) && checkValidBST(root->right, root->val, max)
        return checkValidBST(1, LONG_MIN, 2) && checkValidBST(3, 2, LONG_MAX)

// checkValidBST(1, LONG_MIN, 2)
Step 6: if root == NULL
           false

Step 7: if root->val <= min || root->val >= max
           1 <= LONG_MIN || 1 >= 2
           false || false
           false

Step 8: return checkValidBST(root->left, min, root->val) && checkValidBST(root->right, root->val, max)
        return checkValidBST(null, LONG_MIN, 1) && checkValidBST(null, 1, LONG_MAX)

// checkValidBST(3, 2, LONG_MAX)
Step 9: if root == NULL
           false

Step 10: if root->val <= min || root->val >= max
            2 <= LONG_MIN || 2 >= LONG_MAX
            false || false
            false

Step 11: return checkValidBST(root->left, min, root->val) && checkValidBST(root->right, root->val, max)
         return checkValidBST(null, LONG_MIN, 3) && checkValidBST(null, 3, LONG_MAX)

Now for all the conditions
Step 7: checkValidBST(null, LONG_MIN, 1) && checkValidBST(null, 1, LONG_MAX)
Step 11: checkValidBST(null, LONG_MIN, 3) && checkValidBST(null, 3, LONG_MAX)

the first parameter root is null

So it returns true.

Hence the final answer we return is true.

Comments

[Maksim Glinyanov]

In the Golang code, it is better to use math.MinInt64 and math.MaxInt64 as min and max. Because the usual int in go is int64, and in the condition of the Val task it is int.

[Alkesh Ghorpade]

Thanks for sharing this. I will keep in mind.