EXPLORING THE 4th DIMENSION THROUGH FRACTALS
What I really find beautiful about mathematics , is just how simplicity leads to beautiful results
so lets explore the world of 4 dimensions through the lens of fractals .
So I was just looking for some programming projects , that is when I came across this algorithm
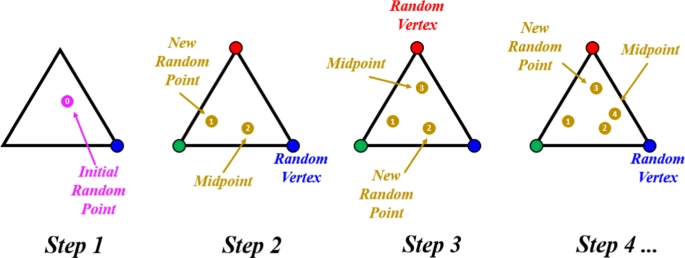
The Chaos Game
Its deceptively simple
You mark Three 2D points say A,B,C to form an equilateral triangle using x,y coordinates then choose any random point on the plane .
A certain set of points which satisfies these properties is for example ,
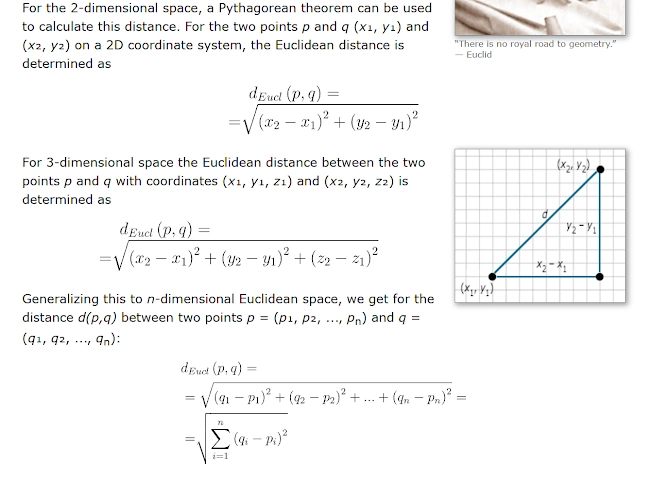
We can verify this using the distance formula for 2d spaces.
Then proceed to mark a third point on the midpoint of the chosen random point and Any of the Points again randomly chosen from the A B or C , using the midpoint formula for 2 dimensional space
And infinitely repeat this process , By placing a point again on the resultant point and randomly chosen point from the three vertices of the triangle
https://www.youtube.com/watch?v=kbKtFN71Lfs&t=458s check out this video for a complete explanation
Now let's apply this to our triangle
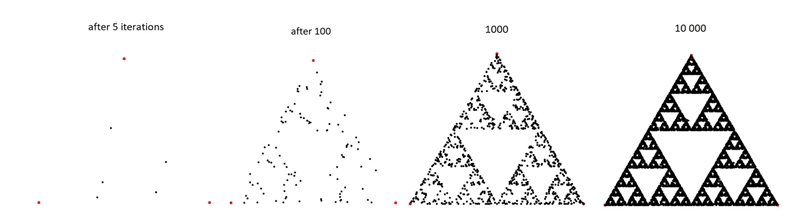
at first it looks like well CHAOS but slowly you see a pattern starts to emerge
What if we arrange the points co linearly ?
What if we start with a square ?
For those of you who are curious ,I leave those questions for you to answer as an programming exercise
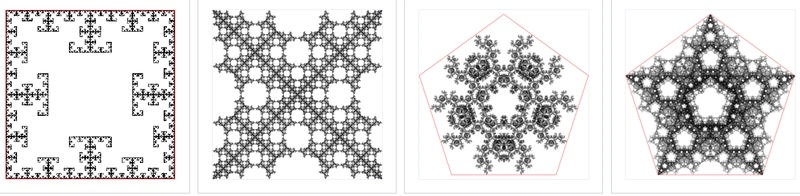
Tweaking these sets of initial points and adding more restrictions gives rise to even more interesting fractals, go ahead and try experimenting
Here are some examples
Notice the element of randomness in this algorithm , yet it produces a beautiful deterministic patterns , tbh I found it very strange at first and you know what's crazy
it forms these fractals in infinite dimensions , but before getting too ahead of ourselves
First lets extend this simple algorithm to Three dimensions
That's right
Instead of a triangle we take a regular tetrahedron which is basically just a triangular pyramid with equal sides and repeat the same process
And again from chaos emerges a sierpinski tetrahedron , These infinitely repeating self similar patterns that you see forming are called fractals.
You see them emerge everywhere in nature from tiny snowflakes to entire galaxies
Crazy stuff !
But now begins the fun part ,
The cool thing with math is you aren't bound by the laws of reality or the limits of human perception , lets dig deeper
So we are going to step it up a notch and extend this same pattern to 4 dimensions
For that we need to first examine a few things
We experience the world within our senses , we experience a 3d world which is then projected on the 2d retina ,
Slowly through evolution our brain has figured out certain tricks .
Like shadows , foreshortening and perspective through which it makes sense of the 3d world and its depth even though we are limited to a 2d retina ,
Artists since millennia have figured out techniques to fool the brain ,the 2d picture they are looking is actually 3d
But sadly our brain has no frame of reference to perceive the fourth dimension
It understands a 3 dimensional world through a 2d retina after all .
First of all let's start with finding the 4 dimensional equivalent of an tetrahedron ,
So let's analyse what did we just do earlier
In 2 dimensions, we defined an equilateral triangle using two coordinates: x,y.
By applying the euclidean distance formula, we ensure that the lengths of all three sides are the same. Where x1,y1 and x2,y2 are the corresponding points on the triangle
Moving to 3 dimensions, we use three coordinates: x,y,z
Again, applying the distance formula ensures the sides are equal, giving us a tetrahedron.
But here’s the exciting part:
We’re not limited to these dimensions
Similarly for finding the Midpoint we can use
Both of these formulas have been derived by extending the patterns from 2d and 3d spaces to an abstract world of n - dimensional Euclidean space .
Similarly ,
In 4 dimensions, we can define a shape with four coordinates: x,y,z,w
.
With the following coordinates
(1,1,1,−1 )
(1,−1,−1,−1)
(−1,1,−1,−1)
(−1,−1,1,−1)
(0,0,0,2)
We can apply the same distance formula to verify if it verifies the property of a equilateral sides , and voilà
It’s the 4-dimensional equivalent of a tetrahedron.
Some of you may be more comfortable with this strange idea of extending the euclidean formula to any n dimensional space
To all of those who are skeptical , with math ,the thing is you just follow the patterns and see where it takes you , so for now i would recommend you all to just follow the patterns and follow beauty and see where it guides you
We can take this abstract 4D figure and apply the same Chaos Game algorithm to it.
Pick a random point in 4D space.
Mark the 5 points of a 4d tetrahedron in 4d coordinates
Choose a random vertex of the 4-simplex.
Mark the midpoint
"Now, I know what you're thinking:
That midpoint that we just found its in 4 dimensions too , now how the heck do we visualise it
How can we see something that's 4-dimensional if we're stuck in 3D?
This is where the beauty of math and art intersect.
think about shadows.
Imagine yourself as a 2-dimensional being, living on a flat plane and you cast light on a 2d object
What would you see ?
A point shadow
Why?
Because a 2-dimensional object, like a line, casts a 1-dimensional shadow. To you, that shadow looks like just a point.
Now, again let's extend this idea to 3d
As 3-dimensional beings, what do we see when we look at an image of a cube on a 2D screen?
We’re looking at its 2D shadow, not the cube itself.
As we discussed earlier
Your brain uses tricks—perspective, foreshortening, shading—to interpret this 2D projection of the 3D object
By now You might have started seeing an idea here , we try to find patterns in 2nd and 3rd dimensions and just blindly trust the math and extend it to 4d
So ,
What would shadow of a 4 d object look like , if we follow the pattern it should create a 3d shadow which could be projected on a 3d space
And there it is , a way for us to visualise the 4 dimensional fractal we just generated
Now the question is How do we cast its shadow , or in other worlds project it onto the 3d plane
Every time we project an object from n-dimensions onto a lower dimension, we lose some information.what I mean by that is that you can not infer every property of an n dimensional object while looking at its n-1 dimensional projection
Like when you look at a cube projected on a 2d screen you can not see all of its edges at once for example as they get hidden by the faces in front of them
This is why There are tons of ways of projection
But each projection system is designed to preserve different aspects of the image.
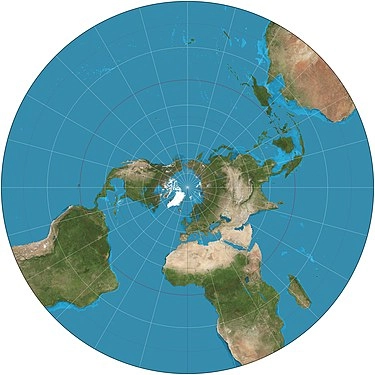
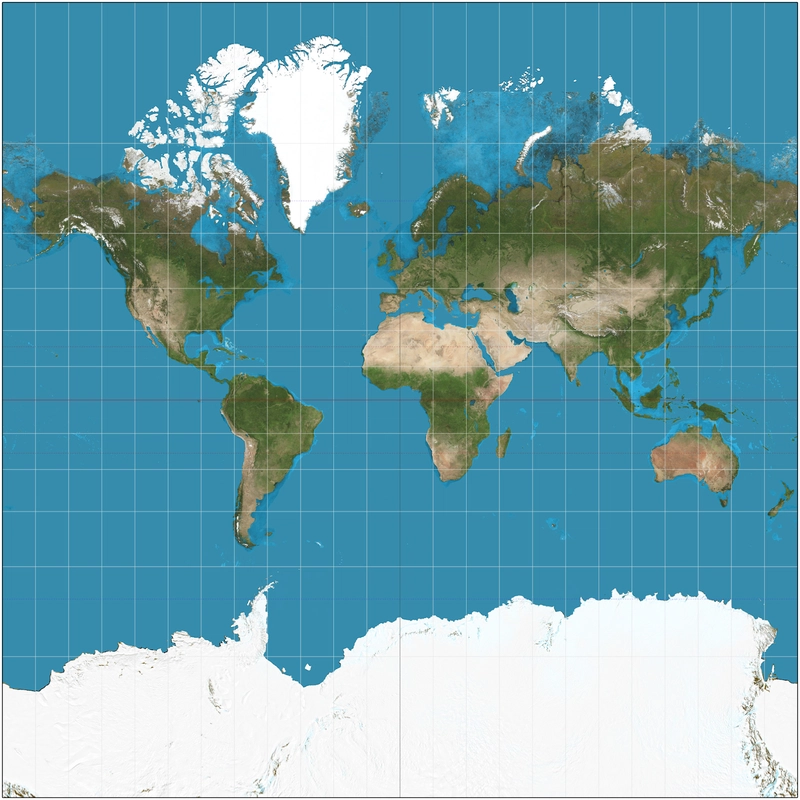
One case where we encounter a similar problem is maps where we need to project an entire 3d spherical earth onto a 2d map
Different projection techniques lead to different results , each giving us some unique insight about the 3d object .
Like the one to left is a stereographic projection , it preserves the circular shape of the globe
And one to the right is a mercator projection which preserves the actual shapes of the countries
now the math involved in these is out of scope of this article , for now just think of it as an formula which takes 3 dimensional inputs and spits an 2 dimensional input
While wrapping our minds around the 4th dimensions , we need to take a similar approach
And that’s the beauty of it.
With math, we can step beyond our sensory limitations, moving through dimensions that our brains simply can’t directly perceive.
We can use projections to reveal parts of the 4-dimensional world, even if we can’t fully understand .
Each projection will reveal something more about our 4d fractal , similar to how each type of projection of a 3d earth reveals different details about it .
Let's start with a stereographic projection , generally it preserves angles at which curves meet and thus approximately preserves shapes.
So obtained 4d points earlier , we can use the following stereographic projection formula which converts our points into 3 dimensional points .
Now that we have tamed the 4-d figure to something we can visualise
Lets repeat the chaos game steps
I got these results
Please feel free to experiment with different shapes , rules and projections methods and explore the world of fractals infinite dimensions
What you are looking at is two 3 dimensional views of a 4 dimensional Sierpinski 5-cell rotated relative to each other , further projected onto your 2d screen
When you look at this fractal, remember: you're not just looking at a shape, but at the hidden beauty extending in theoretically infinite dimensions which we can peek into by seeing the ripples of their majesty in their 3d and 2d projections







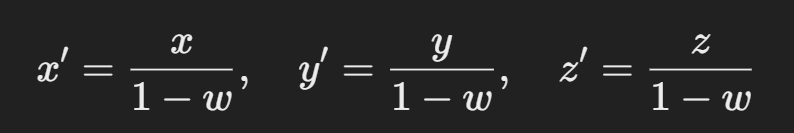



Top comments (2)
Nice, this was interesting to read.
Have you perhaps tried visualizing the 4th dimension as time, so using an animated rendering, instead of a static projection?
Sometimes seeing things move can unlock a lot of new meanings.
good stuff man !