You must be familiar with function composition.
Well, function composition itself is a function right? What do you think will happen when you compose compositions?
It becomes another composition operator that can compose an unary function and a binary function. That is to say,
Now let
be
Then is
We can go one step further and compose three compositions.
It becomes a composition operator that can compose an unary function and a ternary function. In other words, the degree of the domain increases by 1 everytime we compose another composition.
You may be wondering how it is possible. You can try direct proof first to see the mechanism although it won’t tell you much about the idea behind it. I’ll put the brief, outline proof just to make the point of how unhelpful it is.
Signature of function composition is
Both parameters are also composition functions therefore the signatures of are
Therefore the signature of the outcome is
Which is the signature of unary-binary-composition function.
As you can see it doesn’t tell you why. It’s like saying is the slope of the tangent line of without mentioning derivative.
If you know Hom functor then much better explanation is possible.
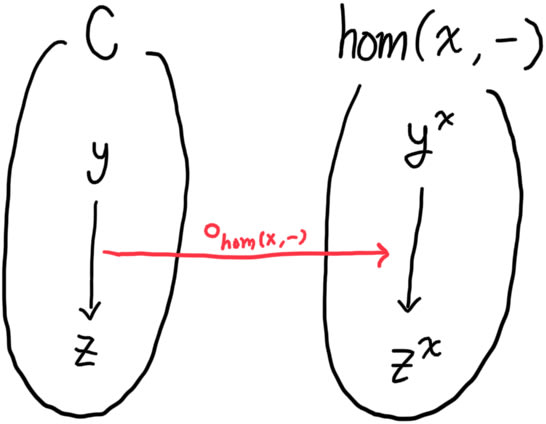
You can consider a function composition as a hom-functor in category theory’s perspective. To present function composition as hom-functor:
If you are not familiar with notation, you can just think of it as a function
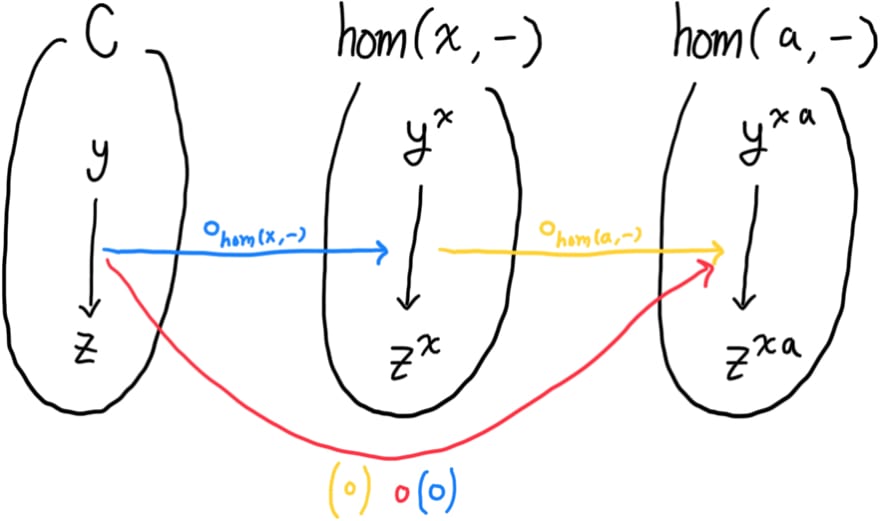
And here’s the composition of two function compositions
You can construct universally with and
Here’s an application in programming. Say you are making a function that calculates a vector’s magnitude. It’s always encouraged to use squared magnitude instead of actual magnitude unless it’s absolutely necessary for performance reasons therefore you have to support both functionalities. You can implement squaredMagnitude first and then implement magnitude by composing sqrt and squaredMagnitude using the discussed method.
(.*) :: (c -> d) -> (a -> b -> c) -> (a -> b -> d)
(.*) = (.) . (.)
squaredMagnitude :: Double -> Double -> Double
squaredMagnitude x y = x^2 + y^2
magnitude = sqrt .* squaredMagnitude
main :: IO ()
main = do
print $ squaredMagnitude 3 4
print $ magnitude 3 4
It outputs
25.0
5.0







Top comments (0)