Understanding Data For Data Analytics, Data Science, and Machine Learning – Part-5

Things to know beforehand

• Random variable: takes values from a sample space; probabilities describe which values and set of values are taken more likely.
• Event: set of possible values (outcomes) of a random variable that occurs with a certain probability.
• Probability function or probability measure: describes the probability P (X ∈ E) that the event E occurs.
• Cumulative distribution function: function evaluating the probability that X will take a value less than or equal to x for a random variable (only for real-valued random variables).

[8]Distribution

A Probability distribution is a mathematical function that, stated in simple terms, can be thought of as providing the probability of occurrence of different possible outcomes in an experiment.

The distributions describe the shape of a batch of numbers that is the meaning of distribution. Suppose the different set of numbers there, you want to show what shape it follows whether it is a bell shaped, we can call it is a normal distribution. If it is forming a rectangular shape, we can call it as a uniform distribution like this that describes the shape of a batch of numbers.

Type of Distributions

there are multiple types of distributions based on it shape and what type of data it represents.

Major distribution to take note of are:

• Binomial Distribution
• Geometric distribution
• Bernoulli distribution
• Poisson distribution
• student's t
• chi-squared
• Uniform

Distribution is divided into two parts based on its data type, i.e., continues and discreet

When you have data on continues, you have to find the area under the curve for your required probability, and if data is discreet you have to use
good old summation.

Probability Density Function

In probability theory, a probability density function, or density of a continuous random variable, is a function whose value at any given sample in the sample space can be interpreted as providing a relative likelihood that the value of the random variable would be close to that sample.

Cumulative distribution function

The cumulative distribution function of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.

In simpler terms, at a point of the curve, it represents the probability of that point to all the preceding points.

$$F_X(x) = P(X\leq x)$$

Binomial Distribution

The binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a yes–no question, and each with its own Boolean-valued outcome: success (with probability p) or failure (with probability q = 1 − p).

A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment, and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance.

$$P_x = \binom{n}{x}P^xq^{n-x}$$

This distribution show the probability of a particular value on

X-axis : values
Y-axis : respected probability

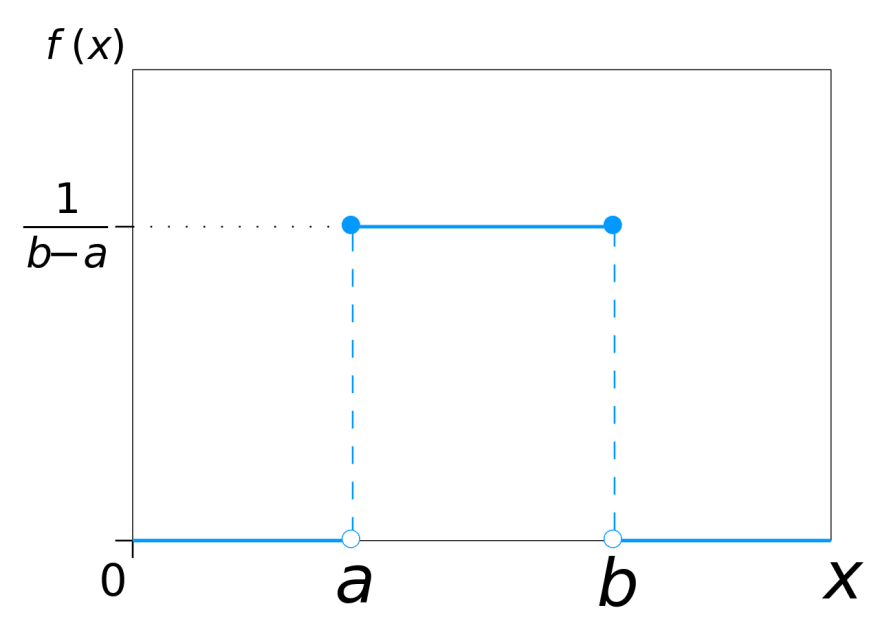
Uniform Distribution

In uniform distribution, probability of occurrence of each event is equivalent to each other.

Poisson Distribution

the Poisson distribution is use when probability of success is very low.

The Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event.

$$Pr(X=k) = \frac{\lambda^ke^{-\lambda}}{k!}$$

where

• k is the number of occurrences (k=0,1,2 …)
• e is Euler's number (e=2.71828...)
• ! is the factorial function.