Understanding Data For Data Analytics, Data Science, and Machine Learning – Part-3

[3] Type Of Data in Statics (Random Variable)

By having different type of random variable in your data, statistical method used in analysis and algorithms used to train will be different.
This type of data can have non-numeric data.

[a] Categorical Data

A categorical variable (also called qualitative variable) is a variable that can take on one of a limited, and usually fixed, number of possible values, assigning each individual or other unit of observation to a particular group or nominal category on the basis of some qualitative property.
Examples of categorical variables are race, sex, age group, and educational level.

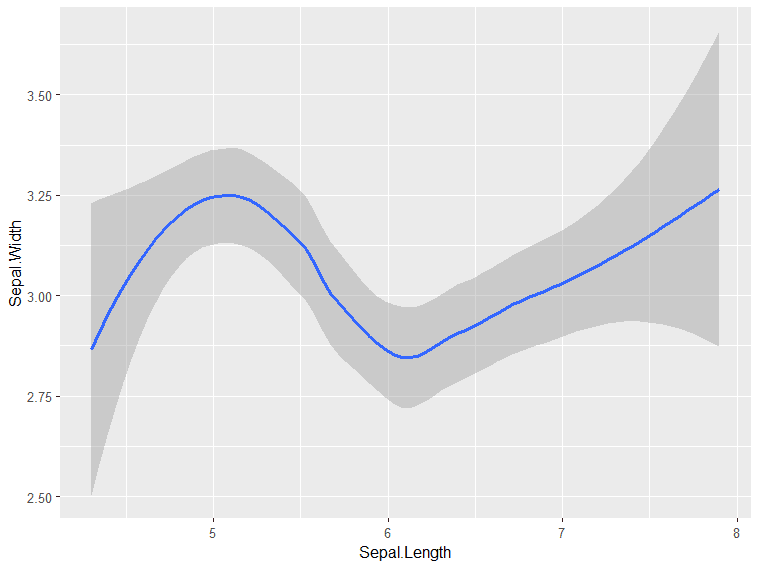
In this example, image Species in a Categorical variable, but Sepal.Length is a Numerical variable.

To convert any data to a categorical data in R

as.factor(data$col)

[1] Nominal Data

These type of variable doesn't have a particular order, or the order doesn't matter.
Example of Nominal Data are sex, race, group, etc.

[2] Ordinal Data

These type of variable does have a particular order, or the order does matter.
Example of Nominal Data are grades, age, size, height, etc.

[b] Numerical Data

This type of data includes data which have only numbers

In this example, both X and Y axes data is numerical.

Generally, you do not need to convert data to numerical because by default it is numeric.

[1] Discrete Data

In Discrete type of data, data can have any value, but it has to be an integer number.
Example, number of person in room, etc.

[2] Continues Data

This type of data can take any type of value, i.e., integers and fractions
for Example, current temperature, distance, etc.

[4] Moments

The moments of a function are quantitative measures related to the shape of the function's graph. If the function represents mass, then the first moment is the center of the mass, and the second moment is the rotational inertia. If the function is a probability distribution, then the first moment is the expected value, the second central moment is the variance, the third standardized moment is the skewness, and the fourth standardized moment is the kurtosis. The mathematical concept is closely related to the concept of moment in physics.

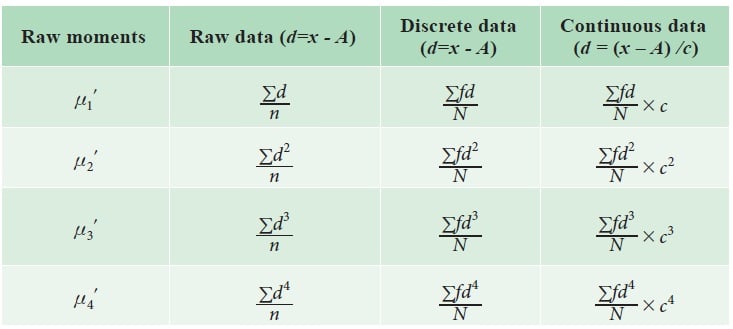
Raw moments:

Raw moments can be defined as the arithmetic mean of various powers of deviations taken from origin. The rth Raw moment is denoted by μr’, r=1,2,3…. Then the first raw moments are given by

Central Moments:

Central moments can be defined as the arithmetic mean of various powers of deviation taken from the mean of the distribution. The rth central moment is denoted by μr, r=1,2,3….

In general, given n observation x1, x2,……., xn  the rth order raw moments (r=0,1,2,…) are defined as follows:

Relation between raw moments and central moments

[5] Kurtosis and Skewness

Kurtosis and Skewness are the 2 value that shows how a distribution looks, i.e., how thin and tall it is and where it has a tail or not respectively.

To calculate kurtosis:

$$Kurt = \frac{\mu_{4}}{\sigma^4}$$

μ4 is 4th central moment
σ is standard deviation

kurtosis(data)
# Kurtosis for above graph 2.422853

To calculate skewness:

$$Skew = \tilde{\mu_{3}} = \frac{\Sigma_{i}^{N}(X_{i} - \overline{X})^3}{(N -1 )* \sigma^3}$$

skewness(data)
# Skewness for above graph is 0.7824835

---

For Part-4 go here

Comments

[Lundeen.Bryan]

Thanks @ishubhamsingh2e this was a great series of articles, I have been trying to brush up on my statistics lately and this helped!

[Shubham Singh]

thank you for your response it's means a lot to me