Radix Sort

" Radix sort is an integer sorting algorithm that sorts data with integer keys by grouping the keys by individual digits that share the same significant position and value (place value). Radix sort uses counting sort as a subroutine to sort an array of numbers." - _{brilliant.org}

Base Numbering Systems

The value of different positions in a number increases by a multiplier of 10 in increasing positions. This means that a digit ‘8’ in the rightmost place of a number is equal to the value 8, but that same digit when shifted left one position (i.e., in 80) is equal to 10 * 8. If you shift it again one position you get 800, which is 10 * 10 * 8.

This is where it’s useful to incorporate the shorthand of exponential notation. It’s important to note that 100 is equal to 1. Each position corresponds to a different exponent of 10.

So why 10? It’s a consequence of how many digits are in our alphabet for numbering. Since we have 10 digits (0-9) we can count all the way up to 9 before we need to use a different position. This system that we used is called base-10 because of that.

Sorting By Radix

So how does a radix sort use this base numbering system to sort integers? First, there are two different kinds of radix sort: most significant digit, or MSD, and least significant digit, or LSD.

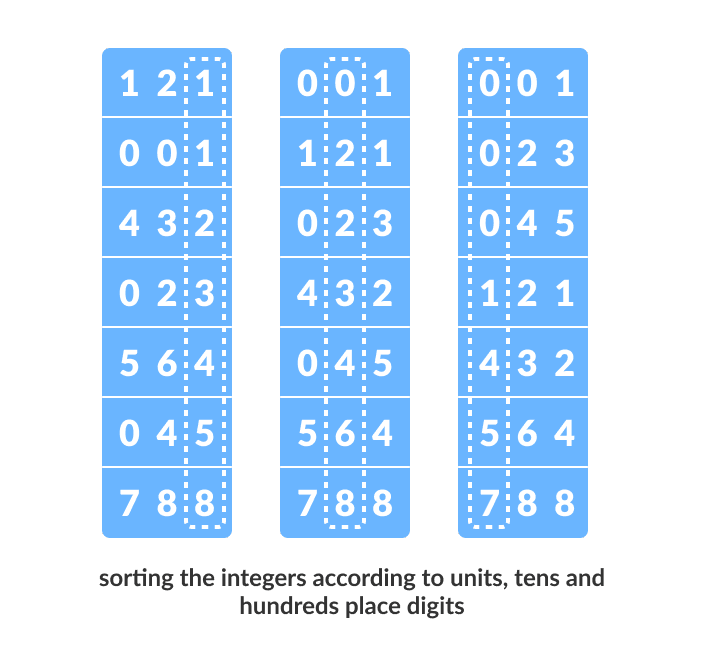
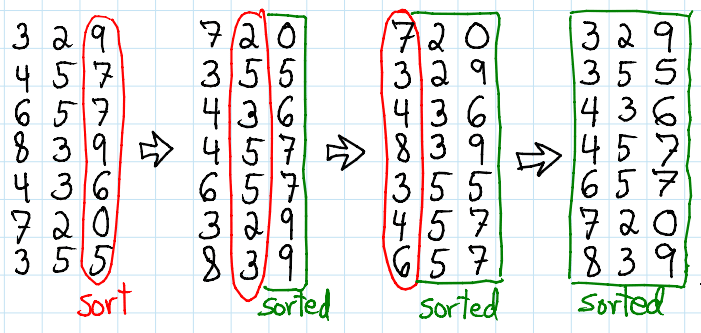
Both radix sorts organize the input list into ten “buckets”, one for each digit. The numbers are placed into the buckets based on the MSD (left-most digit) or LSD (right-most digit). For example, the number 2367 would be placed into the bucket “2” for MSD and into “7” for LSD.

This bucketing process is repeated over and over again until all digits in the longest number have been considered. The order within buckets for each iteration is preserved. For example, the numbers 23, 25 and 126 are placed in the “3”, “5”, and “6” buckets for an initial LSD bucketing. On the second iteration of the algorithm, they are all placed into the “2” bucket, but the order is preserved as 23, 25, 126.

_{Image credits to progamiz.com}

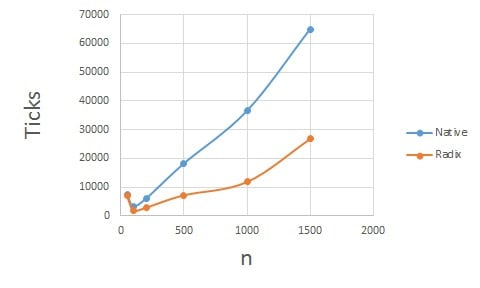
Radix Sort Performance

This makes its performance a little difficult to compare to most other comparison-based sorts. Consider a list of length n. For each iteration of the algorithm, we are deciding which bucket to place each of the n entries into.

How many iterations do we have? Remember that we continue iterating until we examine each digit. This means we need to iterate for how ever many digits we have. We’ll call this average number of digits the word-size or w.

This means the complexity of radix sort is O(wn). Assuming the length of the list is much larger than the number of digits, we can consider w a constant factor and this can be reduced to O(n).