As I've been studying Data Structures and Algorithms for the past week, a repetitive topic I've been seeing in technical interviews on Glassdoor is graph traversals
Overview
Using graphs to model complex networks is pretty swell, but one way that graphs can really come in handy is with graph search algorithms. You can use a graph search algorithm to traverse the entirety of a graph data structure in search of a specific vertex value.
There are two common approaches to using a graph search to progress through a graph:
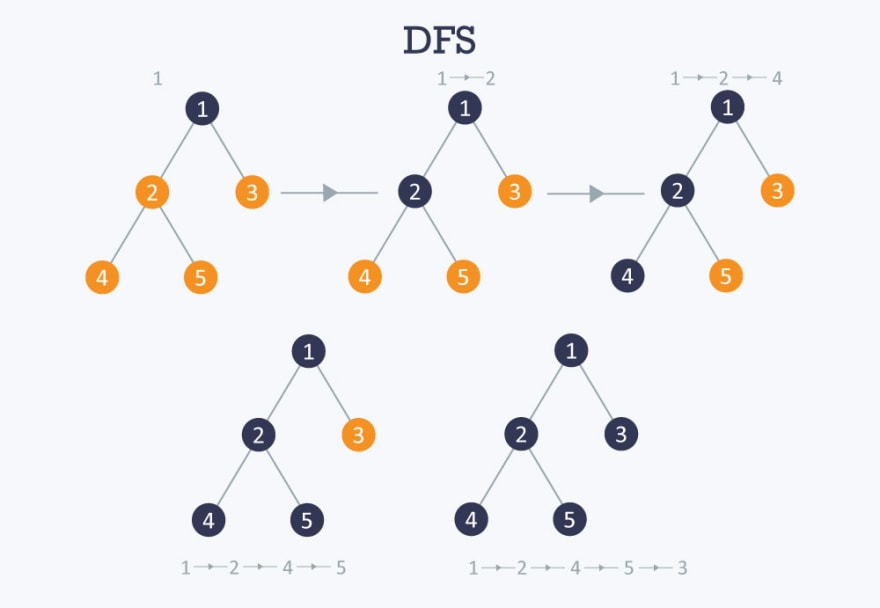
depth-first search, known as DFS follows each possible path to its end
breadth-first search, known as BFS broadens its search from the point of origin to an ever-expanding circle of neighboring vertices
To enable searching, we add vertices to a list, visited. This list is pretty important because it keeps the search from visiting the same vertex multiple times! This is particularly vital for cyclical graphs where you might otherwise end up in an infinite loop.
So how do you calculate the runtime for graph search algorithms?
In an upper bound scenario, we would be looking at every vertex and every edge. Because of this, the big O runtime for both depth-first search and breadth-first search is O(vertices + edges).
Depth-First Search (DFS) Conceptual
Imagine you’re in a car, on the road with your friend, “D.” D is on a mission to get to your destination by process of elimination. D won’t stop and ask for directions. D just sticks to a chosen path until you reach the end.
At that point, if the end wasn’t actually your destination, D brings you back to the last point when there was an intersection and tries another path.
Like your friend D, depth-first search algorithms check the values along a path of vertices before moving to another path.
While this isn’t exactly ideal when you want to find the shortest path between two points, DFS can be very helpful for determining if a path even exists.
In order to accomplish this path-finding feat, DFS implementations use either a stack data structure or, more commonly, recursion to keep track of the path the search is on and the current vertex.
In a stack implementation, the most recently added vertex is popped off the stack when the search has reached the end of the path. Meanwhile, in a recursive implementation, the DFS function is recursively called for each connected vertex.
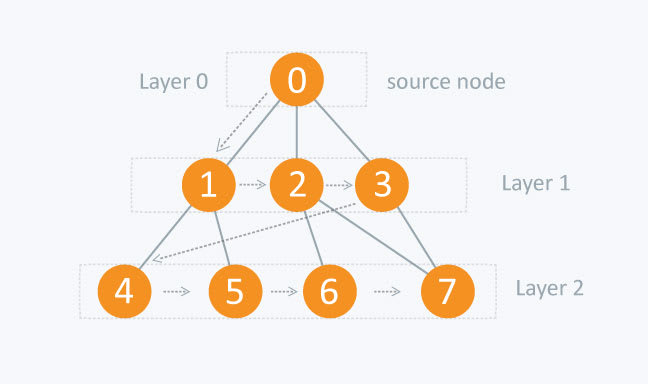
Breadth-First Search (BFS) Conceptual
You’re back in a car, but this time, your friend “B” is navigating. Unlike D, B is a bit hesitant about whether you’ve gone the right way and keeps checking in to see if you are on the best path. At each intersection, B tries out each possible route one by one, but only for a block in each direction to see if you’ve found your destination.
Like B, breadth-first search, known as BFS, checks the values of all neighboring vertices before moving into another level of depth.
This is an incredibly inefficient way to find just any path between two points, but it’s an excellent way to identify the shortest path between two vertices. Because of this, BFS is helpful for figuring out directions from one place to another.
Unlike DFS, BFS graph search implementations use a queue data structure to keep track of the current vertex and vertices that still have unvisited neighbors. In BFS graph search a vertex is dequeued when all neighboring vertices have been visited.
Summary
You’ve learned a bunch about graph searches and how to use them effectively:
- You can use a graph search algorithm to traverse the entirety of a graph data structure to locate a specific value
- Vertices in a graph search include a “visited” list to keep track of whether or not each vertex has been checked
- Depth-first search (DFS) and breadth-first search (BFS) are two common approaches to graph search
- The runtime for graph search algorithms is O(vertices + edges)
- DFS, which employs either recursion or a stack data structure, is useful for determining whether a path exists between two points
- BFS, which generally relies on a queue data structure, is helpful in finding the shortest path between two points
- There are three common traversal orders which you can apply with DFS to generate a list of all values in a graph: pre-order, post-order, and reverse post-order
Depth-First Traversal (One path)
Traversals are incredibly useful when you are trying to find a particular value or a particular path in a graph. We’ll first explore the depth-first traversal function for traversing through a directed graph. To recap, depth-first traversals iterate down each vertex, one neighbor at a time, before going back up and looking at the neighbor’s connected vertices. In this exercise, we will focus on traversing down the full length of one path and logging each vertex’s data value.
For simplicity, we’ll implement the traversal iterator as a separate function instead of as a method on the Graph class. In other implementations, the iterator can be seen as a class method.
We have also set up a sample graph in testGraph.js for you to test the traversals against. Feel free to take a look at the file to familiarize yourself with the structure of the graph.
const depthFirstTraversal = (start, visitedVertices = [start]) => {
console.log(start.data)
if (start.edges.length) {
const neighbor = start.edges[0].end;
if (!visitedVertices.includes(neighbor)) {
visitedVertices.push(neighbor);
depthFirstTraversal(neighbor, visitedVertices);
}
}
};
depthFirstTraversal(testGraph.vertices[0]);
Depth-First Traversal (All paths)
We’ve gotten the hang of traversing down one path, but we want to traverse down all the paths (not just the first possible path). We will modify our existing implementation to iterate down all the other paths by using a .forEach() loop to iterate through all of the start vertex’s edges.
We won’t have to worry about iterating through all the neighbors before going down the neighbor’s first connected vertex. This is because the recursive call occurs before the next iteration of the for loop.
const testGraph = require('./testGraph.js');
const depthFirstTraversal = (start, visitedVertices = [start]) => {
console.log(start.data);
start.edges.forEach(edge => {
const neighbor = edge.end;
if (!visitedVertices.includes(neighbor)) {
visitedVertices.push(neighbor);
depthFirstTraversal(neighbor, visitedVertices);
}
});
};
depthFirstTraversal(testGraph.vertices[0]);
Depth-First Traversal (Callbacks)
Our current implementation of the depth-first traversal simply prints out the vertices of the graph as they are traversed. This would be useful in scenarios where we want to see the order that the traversal occurs in. For example, if the graph was an instruction list, we need the exact order that the steps will occur to determine which dependencies need to be resolved first.
However, there may be other instances where we want to do something other than printing out the traversal order. For example, if we just need to determine if a path exists, like seeing if a maze is solvable, we just need a true or false value. We can do this by opening up a callback parameter for the user.
const depthFirstTraversal = (start, callback, visitedVertices = [start]) => {
callback(start);
start.edges.forEach((edge) => {
const neighbor = edge.end;
if (!visitedVertices.includes(neighbor)) {
visitedVertices.push(neighbor);
depthFirstTraversal(neighbor, callback, visitedVertices);
}
});
};
depthFirstTraversal(testGraph.vertices[0], (vertex) => { console.log(vertex.data) });
Breadth-First Traversal (First layer)
Now it’s time to focus on breadth-first traversal! Just as a reminder, breadth-first iterates through the whole graph in layers by going down one layer, which comprises the start vertex’s direct neighbors. Then it proceeds down to the next layer which consists of all the vertices that are neighbors of the vertices in the previous layer.
For this exercise, let’s focus on traversing down one layer. We will take a similar approach as we did with the depth-first traversal by keeping an array of visitedVertices to prevent us from iterating through the same vertices.
However, we will iterate through all of the direct neighbor vertices instead of iterating down the neighbor’s first edge. We will also use a queue to traverse through the graph instead of recursion to explore the different ways we can implement the traversals.
const breadthFirstTraversal = (start) => {
const visitedVertices = [start];
start.edges.forEach(edge => {
const neighbor = edge.end;
if (!visitedVertices.includes(neighbor)) {
visitedVertices.push(neighbor)
}
});
console.log(visitedVertices)
};
breadthFirstTraversal(testGraph.vertices[0]);
Breadth-First Traversal (All layers)
So far, we can iterate down one layer, but we have yet to iterate down the remaining layers. In order to do so, we will introduce a queue that will keep track of all of the vertices to visit.
As we iterate through the neighbors, we will add its connected vertices to the end of the queue, pull off the next neighbor from the queue, add its connected vertices, and so on. This way allows us to maintain the visiting order; we will visit the vertices across the same layer while queueing up the next layer. When there are no vertices left in the current layer, the vertices of the next layer are already queued up, so we move down and iterate across the next layer.
We will use our implementation of the Queue data structure that was covered in a previous course. It is located in Queue.js. Go ahead and take a quick look to refresh your memory of the data structure and the available methods.
const breadthFirstTraversal = (start) => {
const visitedVertices = [start];
const visitQueue = new Queue();
visitQueue.enqueue(start);
while (!visitQueue.isEmpty()) {
const current = visitQueue.dequeue();
console.log(current.data);
current.edges.forEach((edge) => {
const neighbor = edge.end;
if (!visitedVertices.includes(neighbor)) {
visitedVertices.push(neighbor);
visitQueue.enqueue(neighbor);
}
})
}
};
breadthFirstTraversal(testGraph.vertices[0]);


Top comments (0)