The logic of the XGBoost Classification algorithm is similar to XGBoost Regression, with a few minor differences, like using the Log-Likelihood Loss function, instead of Least Squares and using Probability and Log of Odds in the calculations.
1) Define initial values and hyperparameters.
1a) Define differentiable Loss Function, e.g. 'Negative Log-Likelihood' :
L(yi,pi) =- [yi*ln(pi) +(1-yi)*ln(1-pi)], where
yi- True probabilities (1 or 0), pi - predicted probabilities.
Here we will convert pi to odds and use log of odds when optimizing the objective function.
1b) Assign a value to the initial predicted probabilities (p), by default, it is the same number for all observations, e.g. 0.5.
1c) Assign values to parameters:
learning rate (eta), max_depth, max_leaves, number of boosted rounds etc.
and regularization hyperparameters: lambda, gamma.
Default values in the XG Boost documentation.
2) Build 1 to N number of trees iteratively.
This step is the same as in the XGBoost Regression, where we fit each tree to the residuals.
The difference here:
a) in the formula of the output calculation, where
H = Previous_Probability*[1-Previous_probability].
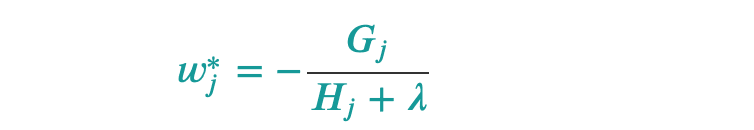
b) we compute new prediction values as
log(new_odds) =log(previos_odds) + eta * output_value
new_probability = e^log(new_odds)/[1+e^log(new_odds)]
3)last step: get final predictions


Top comments (0)