Photo by Markus Spiske on Unsplash
In the previous posts, I described how the Gradient Boosted Trees algorithm works for regression and classification problems. However, for the bigger datasets, the training could be a slow process. Some advanced versions of boosted trees address this issue, like Extreme Gradient Boost (XG Boost), Light GBM, and CatBoost. Here I will give an overview of how the XG Boost works for the regression.
1) Define initial values and hyperparameters.
1a) Define differentiable Loss Function, e.g. 'Least Squares' :
L(yi,pi) =1/2 (yi - pi)^2, where
y-True values, p- predictions
1b) Assign a value to the initial predictions (p), by default, it is the same number for all observations, e.g. 0.5.
1c) Assign values to parameters:
learning rate (eta), max_depth, max_leaves, number of boosted rounds etc.
and regularization hyperparameters: lambda, gamma.
Default values in the XG Boost documentation.
2) Build 1 to N number of trees iteratively.
2a) Get Residuals (yi-pi) to fit observations to the tree
Note:
-Similar to the ordinary Gradient Boosted Trees, we fit trees iteratively to the residuals, not to the predictions.
-Building trees in XG boost a bit different compare to the ordinary regression trees, where we could use gini or entropy to get the gain. In XG boost we use the formula which is derived from the optimization problem of the objective function(objective function is a sum of the loss function and regularization terms).
G - represents sum of gradients (first derivate of a loss function with respect to prediction p), in our case its negative sum of the of the residuals in the leaf (L-left leaf, R-right leaf).
H - second derivative of Loss Function with respect to prediction p, and here equals to number of the residuals
-XG boost allows using a greedy algorithm or approximate greedy algorithm(for bigger datasets) when building the trees and calculating gains.
2c) once we choose the best tree by Gain calculated in the previous step and build the full tree(size of the tree will be limited either by gain values, which also includes gamma for pruning in the formula or by parameters we specified initially).
Now compute the output value for each leaf in the tree.
2d) Compute new prediction values as
new_p =previous_p + eta * output_value
3) get final predictions


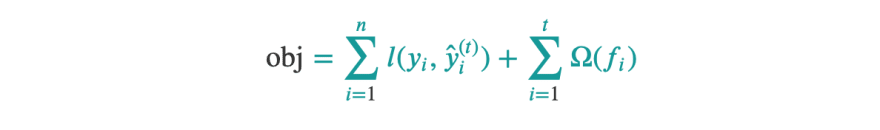



Top comments (0)