What is a Stack?
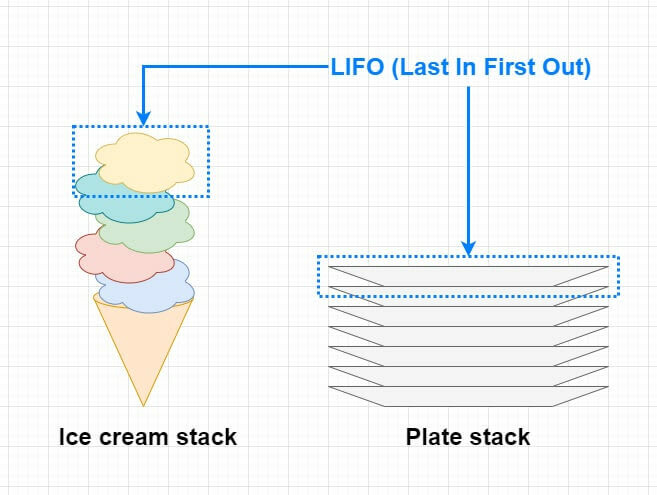
Stack is a linear data structure that stores it's elements in sequential order similar to Arrays. When adding or removing elements, it follows a particular order called LIFO - which is short for Last In First Out.
Easiest way to understand / memorize how Stacks operates with LIFO is to imagining a stack of plates or a stacked ice cream. Anything new that you add will stack on top of eachother. Then whenever you want to retrieve them, you will always start from the top of the stack, then go down one by one until there is no elements left.
Stack is not a built-in data structure in Javascript, but it is simple to implement a custom one.
Anatomy of a Stack
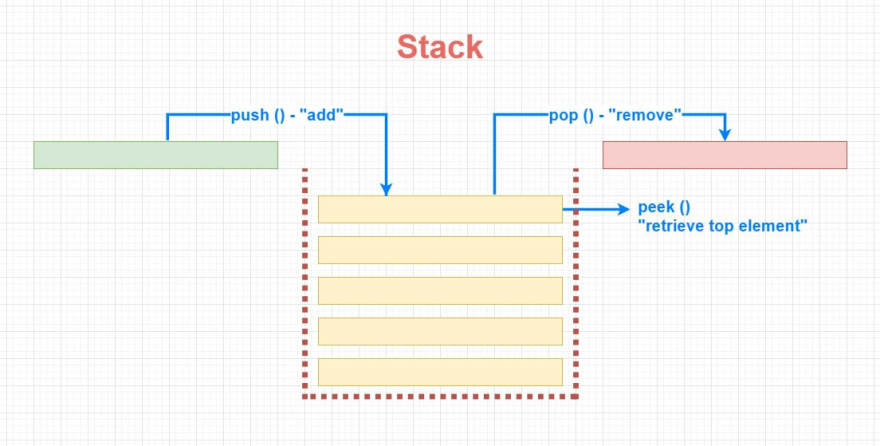
This data structure has quite basic and straight-forward anatomy - we store the elements in sequential order. Whenever we want to add or remove an item from the list of elements, we always work at the very end of the list to follow the LIFO (Last In First Out) order of operations. Similarly, with the peek method we can quickly retrieve the top / latest element in the Stack.
When to use Stack
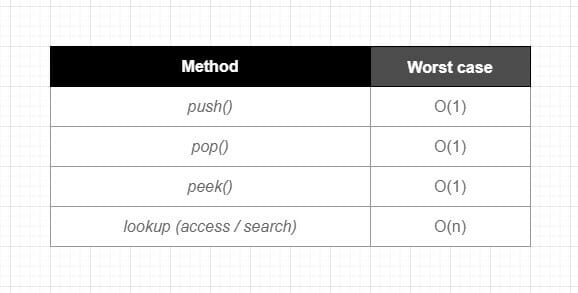
Let’s start with taking a quick look at the Big O of common operations in Stack:
Stack is useful when you specifically want to work with the very last items in a list. For example you want to know the very last item added or need to apply frequent updates just at the end of a list.
Now you maybe thinking, "I can just use a regular array for this instead, why should I even bother with it?". That's what I thought at first as well - and yes an Array can do these operations too. But the point is conceptual difference - if you have noticed the base methods of Stack is very few (pop, push and peek). And that is actually a good thing when you want constrained access to data - or you want to enforce LIFO (Last In First Out) rule of access for your list. Another positive part is having less methods to deal with makes the code easier to understand and work with.
If you need to use lookup / iterations very often, using an Array would be a better choice. Even though you can implement an optional lookup / iterator method to Stack - it won't suit well from a conceptual perspective if you have to use it very often.
Stacks are used in many programming languages and applications in real world. Some examples are:
- Used in Call Stack - which is as a mechanism to keep track of execution order (in simpler words it helps interpreter to navigate through what is happening in our code line by line). In Javascript, if you exceed the memory limit of a browser (an infinite loop can cause this) - in that case you will get a Stack Overflow error that will say "Maximum call stack size exceeded", that's coming from the Call Stack.
- Undo / Redo actions in applications.
- Also used in problem solving concepts like backtracking, reversing words, evaluating arithmetic expressions in programming languages.
Stack implementation in Javascript
Stacks can be implemented using an Array or a Linked List. They are quite close to eachother in terms of performance with different tradeoffs. If you somehow come to a point that you have to choose between them - it would be a choice between better overall performance of Arrays vs better worst-case behaviour of Linked Lists .
Arrays uses cache memory which gives better overall performance. But if an Array is about to reach it's limit, it has to double up it's space in memory to create space for new additions. On the other hand Linked Lists uses dynamic memory and does not need additional empty space, but overall performance is not as good as Arrays since the data is scattered in memory overall the place.
So it all depends on what type of priorities / use case you have - but for the most cases Array is a quite straightforward choice for implementing Stack. I will be sharing both implementations below. For both of them we will be using ES6 Classes to build this data structure. Here is the list of methods in the implementations:
-
push(value)- add to top of Stack -
pop()- remove from top of Stack -
peek()- retrive top element in the Stack -
isEmpty()- helper method to check if Stack is empty -
length()- optional method to check the length of Stack -
clear()- optional method to clear the Stack -
toArray()- optional method returns Stack elements as an Array
I hope this article helped you to understand what Stack is and how it works! I'd like to encourage you to experiment with the implementations below in your favorite code editor. Thanks for reading!
Stack implementation using Array:
class Stack {
constructor() {
this.items = []
}
// add to the top of Stack
push(value) {
this.items.push(value)
}
// remove from the top of Stack
pop() {
if (this.isEmpty()) {
return
}
const removedItem = this.items.pop()
return removedItem
}
// retrive top element in the Stack
peek() {
if (!this.items.length) return
return this.items[this.items.length - 1]
}
// check if Stack is empty
isEmpty() {
return !this.items.length
}
// get the length of Stack
length() {
return this.items.length
}
// clear the Stack
clear() {
this.items = []
}
// return the Stack as an Array
toArray() {
return this.items
}
}
Stack implementation using Linked List:
// Minimal Linked List implementation with: prepend, deleteHead and toArray (optional) methods.
// Since we only need the "beginning of the list" type add & remove operations, there is no need to maintain a tail pointer for this use case. Maintaining a pointer for the head will be enough.
class LinkedListMinimal {
constructor(value) {
this.head = null
this.length = 0
}
// Add to the beginning of list
prepend(value) {
// Initialize a newNode with value recieved and next as null.
const newNode = {
value: value,
next: null
}
// Assign this.head to newNode.next property. Because we are adding to the beginning - and this newNode's next should be pointing to this.head.
newNode.next = this.head
// Now that newNode has the this.head as "next", we can set the this.head as newNode directly.
this.head = newNode
this.length++
}
// Remove from the beginning of list
deleteHead() {
if (!this.head) return
const headVal = this.head.value
// if one element left
if (this.length === 1) {
this.head = null
this.length--
return headVal
}
// define newHead as this.head.next
const newHead = this.head.next
// now change the head pointer to newHead
this.head = newHead
this.length--
return headVal
}
// toArray - loop through nested objects, then return the values in an array
toArray() {
const array = []
// Initialize a currentNode variable pointing to this.head - which will be the starting point for traversal.
let currentNode = this.head
// fill the array until we reach the end of list:
while (currentNode !== null) {
array.push(currentNode.value)
currentNode = currentNode.next
}
return array
}
}
class Stack {
constructor() {
this.items = new LinkedListMinimal()
}
push(value) {
// Pushing means to lay the value on top of the stack. Since we are using a Singly Linked List as an underlying data structure, we can actually do the work at the beginning of the Linked List. Which will be matching to Stack's performance on both addition & deletion - O(1) Constant time
this.items.prepend(value);
}
pop() {
// Pop means remove the value from top of the stack. We just remove the first element (top of the stack) from Linked List by using deleteHead:
if (this.isEmpty()) return
const poppedItem = this.items.deleteHead()
if (!poppedItem) return
return poppedItem
}
peek() {
if (this.isEmpty()) {
return
}
return this.items.head.value
}
isEmpty() {
// The Stack is empty if it's Linked List doesn't have a head.
return !this.items.head
}
length() {
return this.items.length
}
// clear the Stack
clear() {
this.items = new LinkedListMinimal()
}
// return the Stack as an Array
toArray() {
// Note: If you are using your own Linked List and do not have toArray() method, you need to use traversal to output items in Array format.
// Since we only work at the beginning of the Linked List, order of the items will be in reverse order when we output them as an Array. So we need an additional reverse operation right after that to properly convert the Stack into an Array. This will cost O(n + n) => O(2n) => O(n) Linear time, in simpler words the time complexity will be still Linear time (due to LL toArray() method is also being Linear time) at the end even we don't reverse the list.
return this.items.toArray().reverse()
}
}



Top comments (0)