When working with arrays, finding the point of insertion/deletion is constant in time but performing the insertion/deletion is O(n). This potentially costly operation happens since elements in arrays are allocated contiguously in memory, leading to a reorganization of the structure while performing the insertion/deletion.
On the flip side, linked lists, which are comprised of nodes containing a data value and a pointer to the next node (and previous node in the case of doubly linked lists), allow for constant-time insertion/deletion of elements. This performance gain - relative to arrays - occurs since we only need to track the current pointer in memory during traversal and re-assign that pointer when the target element is added or removed.
In other words, regardless of the linked list size, the act of insertion/deletion requires a single action of pointer reassignment, i.e., O(1) time complexity. Though, the traversal to find the element to add/remove has a complexity of O(n). In summary, the time complexities of insertion/deletion between arrays and linked lists are:
Arrays
- Finding the point of insertion/deletion: O(1)
- Performing the point of insertion/deletion: O(n)
Linked Lists
- Finding the point of insertion/deletion: O(n)
- Performing the point of insertion/deletion: O(1)
Let's leap into the world of singly and doubly linked lists.
Singly linked lists
Singly linked lists are defined by nodes, which are plain objects, that contain two properties:
- A value, such as an integer or a string
- A pointer to the next node in the list, or null if at the end of the list.
The list itself also has two properties:
- A head whose value points to the first node in the list
- A length
For instance, a singly linked list with three nodes containing the values of 5, 8, and 13 looks like:
Creating Node and SinglyLinkedList Classes
Using ES6 classes as syntactic sugar for prototypal inheritance, we can start by defining classes for nodes and the singly linked list structure.
Each Node in the list is instantiated with some value (e.g. an integer) and an initial next property set to null.
class Node {
constructor(value) {
this.value = value;
this.next = null;
}
}
A new instance of Node is created with the new operator and the desired value passed into it:
const node = new Node(5);
console.log(node);
// Node { value: 5, next: null }
The list is instantiated by defining two properties: a head that initially is set to null and a length that is initially zero.
class SinglyLinkedList {
constructor() {
this.head = null;
this.length = 0;
}
// Methods to be added next
add(value) {}
addAt(k, value) {}
remove(value) {}
removeAt(k) {}
indexOf(value) {}
nodeAt(k) {}
}
const sll = new SinglyLinkedList();
console.log(sll);
// SinglyLinkedList { head: null, length: 0 }
A new instance of SinglyLinkedList is created with the new operator:
const sll = new SinglyLinkedList();
Adding Nodes
Adding a node at the end of a singly linked list takes the following steps:
- Create a new node with the inputted value.
- Check if the list is empty, i.e., the
headisnull. - If empty, set the list's head to the new node.
- If not empty, traverse the list until the last node (which has a
nextvalue ofnull) is found, then set the last node'snextproperty to point to the new node. - Increment the list's length.
add(value) {
const node = new Node(value);
if (!this.head) {
this.head = node;
} else {
let current = this.head;
while (current.next) {
current = current.next;
}
current.next = node;
}
this.length++;
}
//
const sll = new SinglyLinkedList();
sll.add(5);
sll.add(8);
sll.add(13);
console.log(JSON.stringify(sll, null, 4))
// {
// "head": {
// "value": 5,
// "next": {
// "value": 8,
// "next": {
// "value": 13,
// "next": null
// }
// }
// },
// "length": 3
// }
Adding Node at Index k
Adding a node at an index k is accomplished with the following steps:
- Ensure that index k is non-negative and less than the list's length.
- Create a new node with the inputted value.
- If k = 0, set the new node's
nextvalue to the initialnextvalue of the list'sheadand reassign theheadto the new node. - If k > 0, loop k times starting at the
headand track thepreviousandcurrentnodes during the traversal. These nodes are used to bracket the new node in the next step. - Set the
previousnode'snextvalue to the new node and the new node'snextvalue to thecurrentnode. - Increment the list's length.
addAt(k, value) {
if (k < 0 || k > this.length) {
return false;
}
const node = new Node(value);
if (k === 0) {
node.next = this.head.next;
this.head = node;
} else {
let current = this.head;
let previous = undefined;
for (let i = 0; i < k; i++) {
previous = current;
current = current.next;
}
previous.next = node;
node.next = current;
}
this.length++
}
// Example --
const sll = new SinglyLinkedList();
sll.add(5);
sll.add(8);
sll.add(13);
sll.addAt(2, 10);
console.log(JSON.stringify(sll, null, 4));
// {
// "head": {
// "value": 5,
// "next": {
// "value": 8,
// "next": {
// "value": 10,
// "next": {
// "value": 13,
// "next": null
// }
// }
// }
// },
// "length": 4
// }
Removing Nodes
Removing nodes with a specific value is accomplished in the following steps:
- If the target value is the value of the
head, point theheadto thenextvalue of theheadand decrement the list's length. - Otherwise, traverse the list - tracking the
previousandcurrentnodes - until the target node's value is reached. - Set the
previousnode'snextvalue to thecurrentnode'snextvalue. - Decrement the list's length.
remove(value) {
if (value === this.head) {
this.head = this.head.next;
this.length--;
} else {
let current = this.head;
let previous = undefined;
while (current.next) {
// Traverse until target value found or end of list when current.next === null
if (current.value === value) {
previous.next = current.next;
this.length--;
break;
}
}
}
}
// Example --
const sll = new SinglyLinkedList();
sll.add(5);
sll.add(8);
sll.add(13);
sll.addAt(2, 10);
sll.remove(8);
console.log(JSON.stringify(sll, null, 4));
// {
// "head": {
// "value": 5,
// "next": {
// "value": 10,
// "next": {
// "value": 13,
// "next": null
// }
// }
// },
// "length": 3
// }
Removing Nodes at Index k
Removing nodes at index k is accomplished in the following steps:
- Ensure that k is non-negative and less than the list's length.
- If k === 0, re-set the
headto point to it'snextvalue and decrement the list's length. - If k > 0, traverse the list k times - keeping track of the
previousandcurrentnode - and then set thepreviousnode'snextvalue to thecurrentnode's next value. Decrement the list.
removeAt(k) {
if (k < 0 || k > this.length) {
return false;
}
if (k === 0) {
this.head = this.head.next;
this.length--;
} else {
let current = this.head;
let previous = undefined;
for (let i = 0; i < k; i++) {
previous = current;
current = current.next;
}
previous.next = current.next;
this.length--;
}
}
// Example --
const sll = new SinglyLinkedList();
sll.add(5);
sll.add(8);
sll.add(13);
sll.removeAt(1);
console.log(JSON.stringify(sll, null, 4));singlyLinkedList.js
// {
// "head": {
// "value": 5,
// "next": {
// "value": 13,
// "next": null
// }
// },
// "length": 2
// }
The Index of a Value
Locating the index associated with a certain value is accomplished by simply traversing the list until the target value is found and returning how many steps the traversal required. If no value is found we can return -1 or something similar.
indexOf(value) {
let i = 0;
let current = this.head;
while (i < this.length) {
if (current.value === value) {
return i;
}
current = current.next;
i++;
}
return -1;
}
// Example --
const sll = new SinglyLinkedList();
sll.add(5);
sll.add(8);
sll.add(13);
console.log(sll.indexOf(5)); // 0
console.log(sll.indexOf(8)); // 1
console.log(sll.indexOf(13)); // 2
The Node at Index k
Locating the node at a particular index is accomplished by simply traversing the list k times and returning the resulting node. As done before, we also first check to make sure a valid index is provided.
nodeAt(k) {
if (k < 0 || k > this.length - 1) {
return false;
}
let current = this.head;
for (let i = 0; i < k; i++) {
current = current.next;
}
return current;
}
// Example --
const sll = new SinglyLinkedList();
sll.add(5);
sll.add(8);
sll.add(13);
console.log(JSON.stringify(sll.nodeAt(1), null, 4));
// {
// "value": 8,
// "next": {
// "value": 13,
// "next": null
// }
// }
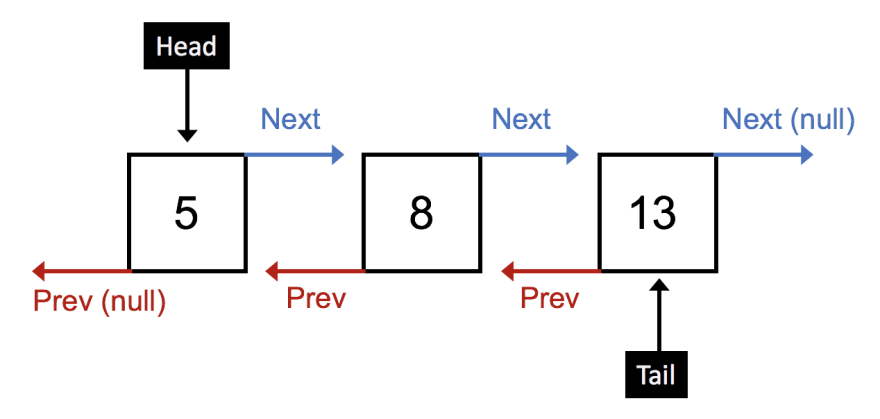
Doubly Linked Lists
We saw that only forward traversal (starting at the head) was possible in singly linked lists. Enabling forward and backward traversal is possible by adding a previous or prev property to each node and a tail property to the linked list. The result is a doubly linked list and conceptually looks like:
Creating Node and DoublyLinkedList Classes
Each Node in the list is instantiated with some value (e.g., an integer) and next and prev properties set to null.
class Node {
constructor(value) {
this.value = value;
this.next = null;
this.prev = null;
}
}
The list is instantiated by defining three properties: a head and tail that initially are set to null and a length that is initially zero.
class SinglyLinkedList {
constructor() {
this.head = null;
this.tail = null;
this.length = 0;
}
// New methods to be added next
display() {}
addAtHead(value) {}
addAtTail(value) {}
addAtIndex(k, value) {}
addAtElement(element, value) {}
removeAtHead() {}
removeAtTail() {}
removeAtIndex(k) {}
removeAtElement(element) {}
}
const dll = new DoublyLinkedList();
console.log(dll);
// DoublyLinked { head: null, tail: null, length: 0 }
Displaying the List
Logging a doubly linked list to the console is a bit tricky due to the circuitous nature of the the prev pointers. I prefer to display the head, tail, and each node on new lines surrounded by arrows representing their prev and next properties:
display() {
let dataString = 'Head => ' + '\n';
let current = this.head;
while (current !== null) {
dataString += '<-' + current.value + '->' + '\n';
current = current.next;
}
dataString += '<= Tail';
return dataString;
}
Adding Nodes at the Head
Adding nodes at the head of the list is accomplished in the following steps:
- If the list is empty, point the head and tail to the new node.
- If the list is not empty:
- Set the new node's
nextproperty to the head's current value (i.e., the current first node in the list). - Set the current first node's
prevproperty (this.head.prev) to the new node. - Reset the head to point to the new node.
- Set the new node's
- Increment the list's length.
addAtHead(value) {
let node = new Node(value);
if (!this.head) {
// First node
this.head = node;
this.tail = node;
} else {
node.next = this.head;
this.head.prev = node;
this.head = node;
}
this.length++;
}
// -- Example
const dll = new DoublyLinkedList();
dll.addAtHead(13);
dll.addAtHead(8);
dll.addAtHead(5);
console.log(dll.display());
// Head =>
// <-5->
// <-8->
// <-13->
// <= Tail
Addings Nodes at the Tail
Adding nodes at the tail is nearly identical to adding at the head:
- If the list is empty, point the head and tail to the new node.
- If the list is not empty:
- Set the new node's
prevproperty to the tail's current value (i.e., the current last node in the list) - Set the current last node's
nextproperty (this.tail.next) to the new node. - Reset the tail to point to the new node.
- Set the new node's
- Increment the list's length.
addAtTail(value) {
let node = new Node(value);
if (!this.tail) {
// First node
this.tail = node;
this.head = node;
} else {
node.prev = this.tail;
this.tail.next = node;
this.tail = node;
}
this.length++;
}
// -- Example
const dll = new DoublyLinkedList();
dll.addAtHead(13);
dll.addAtHead(8);
dll.addAtHead(5);
dll.addAtTail(22);
console.log(dll.display());
// Head =>
// <-5->
// <-8->
// <-13->
// <-22->
// <= Tail
Adding Nodes at Index k
Adding new nodes at a specified index k is accomplished by:
- Checking that the index is non-zero and less than the list's length
- If k = 0, we're at the beginning of the list, so the new node is inserted at the head (see steps above for
addAtHead()) - If k = the list's length, we're at the end of the list, so the new node is inserted at the tail (see steps above for
addAtTail()) - Otherwise, traverse k steps forward from the head (as shown below) or backward from the tail and track the current head in each step. Then:
- Set the new node's
prevproperty to the current head at the end of the traversal - Set the new node's
nextproperty to thenextproperty of the current node - Set the current node's
nextproperty to the new node
- Set the new node's
- Increment the list's length.
addAtIndex(k, value) {
const node = new Node(value);
if (k < 0 || k > this.length) return undefined;
if (k === 0) {
// at head
node.next = this.head;
this.head.prev = node;
this.head = node;
} else if (k === this.length - 1) {
// at tail
node.prev = this.tail;
this.tail.next = node;
this.tail = node;
} else {
//somewhere in the body
let i = 1;
let current = this.head;
while (current.next) {
if (i === k) {
node.prev = current;
node.next = current.next;
current.next = node;
}
current = current.next;
i++;
}
}
this.length++;
}
// -- Example
const dll = new DoublyLinkedList();
dll.addAtHead(13);
dll.addAtHead(8);
dll.addAtHead(5);
dll.addAtTail(22);
dll.addAtIndex(2, 10);
console.log(dll.display());
// Head =>
// <-5->
// <-8->
// <-10->
// <-13->
// <-22->
// <= Tail
Adding Nodes at an Element
Adding nodes at target element is even easier than adding at a target index. We simply traverse the list until the target element is found, tracking the current node at each step, and then:
- Set the new node's
prevproperty to the current node. - Set the new node's
nextproperty to the value current node'snextproperty. - Set the current node's
nextvalue to the current node. - Increment the list's length.
addAtElement(element, value) {
const node = new Node(value);
let current = this.head;
while (current.value !== element && current.next) {
current = current.next;
}
node.prev = current;
node.next = current.next;
current.next = node;
this.length++;
}
// -- Example
const dll = new DoublyLinkedList();
dll.addAtHead(13);
dll.addAtHead(8);
dll.addAtHead(5);
dll.addAtTail(22);
dll.addAtIndex(2, 10);
dll.addAtElement(5, 7);
console.log(dll.display());
// Head =>
// <-5->
// <-7->
// <-8->
// <-10->
// <-13->
// <-22->
// <= Tail
Removing Nodes at the Head
To remove a node at the head, we essentially skip over the first element in the list. This is done by:
- Moving the head to its
nextvalue. - Setting the
prevproperty of the node that the head is now pointed at tonull. - Decrementing the list's length.
removeAtHead() {
if (this.head) {
this.head = this.head.next;
this.head.prev = null;
this.length--;
}
}
// -- Example
const dll = new DoublyLinkedList();
dll.addAtHead(13);
dll.addAtHead(8);
dll.addAtHead(5);
dll.removeAtHead();
console.log(dll.display());
// Head =>
// <-8->
// <-13->
// <= Tail
Removing Nodes at the Tail
To remove a node at the tail, we essentially skip over the last element in the list. This is done by:
- Moving the tail to the tail's
prevnode. - Setting the
nextproperty of the node that the tail is now pointing at tonull. - Decrementing the list's length.
removeAtTail() {
if (this.tail) {
this.tail = this.tail.prev;
this.tail.next = null;
this.length--;
}
}
// -- Example
const dll = new DoublyLinkedList();
dll.addAtHead(13);
dll.addAtHead(8);
dll.addAtHead(5);
dll.removeAtTail();
console.log(dll.display());
// Head =>
// <-5->
// <-8->
// <= Tail
Removing Nodes at Index k
When removing nodes at a target index k, we first check to make sure k is non-negative and less than the list's length. Then:
- If k = 0, we're at the head, call
removeAthead() - If k = list's length, we're at the tail, call
removeAtTail() - Otheriwse, traverse k steps, tracking the current node during each step, and then essentially skip over the node to be removed by:
- Setting the current node's
prev.nextvalue to the current node'snextvalue. - Setting the current node's
next.prevvalue to the current node'sprevvalue.
- Setting the current node's
- Decrement the list's length.
removeAtIndex(k) {
if (k < 0 || k > this.length - 1) {
return undefined;
}
if (k === 0) {
// at the head
this.removeAtHead();
} else if (k === this.length - 1) {
// at the tail
this.removeAtTail();
} else {
let current = this.head;
for (let i = 0; i < k; i++) {
previous = current;
current = current.next;
}
current.prev.next = current.next;
current.next.prev = current.prev;
}
this.length--;
}
// -- Example
const dll = new DoublyLinkedList();
dll.addAtHead(13);
dll.addAtHead(8);
dll.addAtHead(5);
dll.removeAtIndex(1);
console.log(dll.display());
// Head =>
// <-5->
// <-13->
// <= Tail
Removing Nodes at Target Element
Finally, we can remove at a desired element using the following steps:
- If the element to be removed is attached to the node that the
headis pointing to, callremoveAtHead() - If the value to be removed is attached to the node that the
tailis pointing to, callremoveAtTail() - Otherwise, traverse the list until that element is found, tracking the current node during each step, and applying the same logic as above when removing at a desired index.
- Decrement the list's length.
removeAtElement(element) {
if (element === this.head.value) {
this.removeAtHead();
} else if (element === this.tail.value) {
this.removeAtTail();
} else {
let current = this.head;
while (current.value !== element && current.next) {
current = current.next;
}
current.prev.next = current.next;
current.next.prev = current.prev;
this.length--;
}
}
// -- Example
const dll = new DoublyLinkedList();
dll.addAtHead(13);
dll.addAtHead(8);
dll.addAtHead(5);
dll.removeAtElement(8);
console.log(dll.display());
// Head =>
// <-5->
// <-13->
// <= Tail




Top comments (0)