Grading a Multiple-Choice Test
The problem is to write a program that will grade multiple-choice tests. Suppose you need to write a program that grades multiple-choice tests. Assume there are eight students and ten questions, and the answers are stored in a two-dimensional array. Each row records a student’s answers to the questions, as shown in the following array.
Students’ Answers to the Questions:
The key is stored in a one-dimensional array:
Key to the Questions:
Your program grades the test and displays the result. It compares each student’s answers with the key, counts the number of correct answers, and displays it. Below is the program:
Student 0's correct count is 7
Student 1's correct count is 6
Student 2's correct count is 5
Student 3's correct count is 4
Student 4's correct count is 8
Student 5's correct count is 7
Student 6's correct count is 7
Student 7's correct count is 7
The statement in lines 7–16 declares, creates, and initializes a two-dimensional array of characters and assigns the reference to answers of the char[][] type. The statement in line 19 declares, creates, and initializes an array of char values and assigns the reference to keys of the char[] type. Each row in the array answers stores a student’s answer, which is graded by comparing it with the key in the array keys. The result is displayed immediately after a student’s answer is graded.
Finding the Closest Pair
This section presents a geometric problem for finding the closest pair of points. Given a set of points, the closest-pair problem is to find the two points that are nearest to each other. In the figure below, for example, points (1, 1) and (2, 0.5) are closest to each other. There are several ways to solve this problem. An intuitive approach is to compute the distances between all pairs of points and find the one with the minimum distance.
package demo;
import java.util.Scanner;
public class FindNearestPoints {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
System.out.print("Enter the number of points: ");
int numberOfPoints = input.nextInt();
// Create an array to store points
double[][] points = new double[numberOfPoints][2];
System.out.print("Enter " + numberOfPoints + " points: ");
for(int i = 0; i < points.length; i++) {
points[i][0] = input.nextDouble();
points[i][1] = input.nextDouble();
}
// p1 and p2 are the indices in the points' array
int p1 = 0, p2 = 1; // Initial two points
double shortestDistance = distance(points[p1][0], points[p1][1], points[p2][0], points[p2][1]); // Initialize shortestDistance
// Compute distance for every two points
for(int i = 0; i < points.length; i++) {
for(int j = i + 1; j < points.length; j++) {
double distance = distance(points[i][0], points[i][1], points[j][0], points[j][1]); // Find distance
if(shortestDistance > distance) {
p1 = i; // Update p1
p2 = j; // Update p2
shortestDistance = distance; // Update shortestDistance
}
}
}
// Display result
System.out.println("The clostest two points are (" + points[p1][0] + ", " + points[p1][1] + ") and (" + points[p2][0] + ", " + points[p2][1] + ")");
}
/** Compute the distance between two points (x1, y1) and (x2, y2) */
public static double distance(double x1, double y1, double x2, double y2) {
return Math.sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1));
}
}
Enter the number of points: 8
Enter 8 points: -1 3 -1 -1 1 1 2 0.5 2 -1 3 3 4 2 4 -0.5
The closest two points are (1, 1) and (2, 0.5)
The program prompts the user to enter the number of points (lines 8–9). The points are read from the console and stored in a two-dimensional array named points (lines 14–17). The program uses the variable shortestDistance (line 21) to store the distance between the two nearest points, and the indices of these two points in the points array are stored in p1 and p2 (line 20).
For each point at index i, the program computes the distance between points[i] and points[j] for all j > i (lines 24–34). Whenever a shorter distance is found, the variable shortestDistance and p1 and p2 are updated (lines 28–32).
The distance between two points (x1, y1) and (x2, y2) can be computed using the formula sqrt((x2 - x1) ^ 2 + (y2 - y1) ^ 2) (lines 41–43). The program assumes that the plane has at least two points. You can easily modify the program to handle the case if the plane has zero or one point. Note that there might be more than one closest pair of points with the same minimum distance. The program finds one such pair.
It is cumbersome to enter all points from the keyboard. You may store the input in a file, say FindNearestPoints.txt, and compile and run the program using the following command:
java FindNearestPoints < FindNearestPoints.txt
Sudoku
The problem is to check whether a given Sudoku solution is correct. This section presents an interesting problem of a sort that appears in the newspaper every day. It is a number-placement puzzle, commonly known as Sudoku. This is a very challenging problem. To make it accessible to the novice, this section presents a simplified version of the Sudoku problem, which is to verify whether a Sudoku solution is correct.
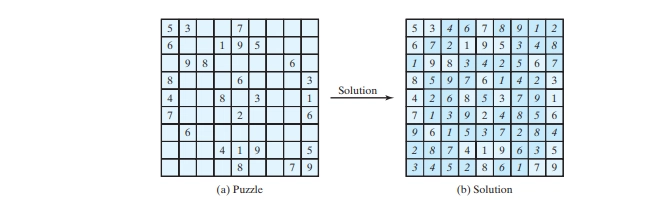
Sudoku is a 9 * 9 grid divided into smaller 3 * 3 boxes (also called regions or blocks), as shown in figure below (a). Some cells, called fixed cells, are populated with numbers from 1 to 9. The objective is to fill the empty cells, also called free cells, with the numbers 1 to 9 so that every row, every column, and every 3 * 3 box contains the numbers 1 to 9, as shown in figure below (b).
For convenience, we use value 0 to indicate a free cell, as shown in figure below (a). The grid can be naturally represented using a two-dimensional array, as shown in figure below (b).
To find a solution for the puzzle, we must replace each 0 in the grid with an appropriate number from 1 to 9. For the solution to the puzzle in figure above, the grid should be as shown in figure below.
Once a solution to a Sudoku puzzle is found, how do you verify that it is correct? Here are two approaches:
- Check if every row has numbers from 1 to 9, every column has numbers from 1 to 9, and every small box has numbers from 1 to 9.
- Check each cell. Each cell must be a number from 1 to 9 and the cell must be unique on every row, every column, and every small box.
The program below prompts the user to enter a solution and reports whether it is valid. We use the second approach in the program to check whether the solution is correct.
package demo;
import java.util.Scanner;
public class CheckSudokuSolution {
public static void main(String[] args) {
// Read a Sudoku solution
int[][] grid = readASolution();
System.out.println(isValid(grid) ? "Valid solution" : "Invalid solution");
}
/** Read a Sudoku solution from the console */
public static int[][] readASolution() {
// Create a Scanner
Scanner input = new Scanner(System.in);
System.out.println("Enter a Sudoku puzzle solution:");
int[][] grid = new int[9][9];
for(int i = 0; i < 9; i++)
for(int j = 0; j < 9 ; j++)
grid[i][j] = input.nextInt();
return grid;
}
/** Check whether a solution is valid */
public static boolean isValid(int[][] grid) {
for(int i = 0; i < 9; i++)
for(int j = 0; j < 9; j++)
if(grid[i][j] < 1 || grid[i][j] > 9 || !isValid(i, j, grid))
return false;
return true; // The solution is valid
}
/** Check whether grid[i][j] is valid in the grid */
public static boolean isValid(int i, int j, int[][] grid) {
// Check whether grid[i][j] is unique in i's row
for(int column = 0; column < 9; column++)
if(column != j && grid[i][column] == grid[i][j])
return false;
// Check whether grid[i][j] is unique in j's column
for(int row = 0; row < 9; row++)
if(row != i && grid[row][j] == grid[i][j])
return false;
// Check whether grid[i][j] is unique in the 3-by-3 box
for(int row = (i / 3) * 3; row < (i / 3) * 3 + 3; row++)
for(int col = (j / 3) * 3; col < (j / 3) * 3 + 3; col++)
if(row != i && col != j && grid[row][col] == grid[i][j])
return false;
return true; // The current value at grid[i][j] is valid
}
}
Enter a Sudoku puzzle solution:
9 6 3 1 7 4 2 5 8
1 7 8 3 2 5 6 4 9
2 5 4 6 8 9 7 3 1
8 2 1 4 3 7 5 9 6
4 9 6 8 5 2 3 1 7
7 3 5 9 6 1 8 2 4
5 8 9 7 1 3 4 6 2
3 1 7 2 4 6 9 8 5
6 4 2 5 9 8 1 7 3
Valid solution
The program invokes the readASolution() method (line 8) to read a Sudoku solution and return a two-dimensional array representing a Sudoku grid.
The isValid(grid) method checks whether the values in the grid are valid by verifying that each value is between 1 and 9 and that each value is valid in the grid (lines 28–34).
The isValid(i, j, grid) method checks whether the value at grid[i][j] is valid. It checks whether grid[i][j] appears more than once in row i (lines 39–41), in column j (lines 44–46), and in the 3 * 3 box (lines 49–52).
How do you locate all the cells in the same box? For any grid[i][j], the starting cell of the 3 * 3 box that contains it is grid[(i / 3) * 3][(j / 3) * 3], as illustrated in figure below.
With this observation, you can easily identify all the cells in the box. For instance, if grid[r][c] is the starting cell of a 3 * 3 box, the cells in the box can be traversed in a nested loop as follows:
// Get all cells in a 3-by-3 box starting at grid[r][c]
for (int row = r; row < r + 3; row++)
for (int col = c; col < c + 3; col++)
// grid[row][col] is in the box
It is cumbersome to enter 81 numbers from the console. When you test the program, you may store the input in a file, say CheckSudokuSolution.txt, and run the program using the following command:
java CheckSudokuSolution < CheckSudokuSolution.txt










Top comments (0)