Intro
A hash table is a data structure that contains key, value pairs. Hash tables use something called a hash function to store and retrieve the data. The hashing function will allow you to map the key to a hash code in order to retrieve the index for the data you are looking for. This is similar to the Dewey Decimal System in a library where books are looked up based on a decimal number. With this system, books are categorized by genre and assigned a number within a specific range.
Stored Data
Hash tables have a predetermined length, where each of the cells stores a key value pair. These cells are usually referred to as "buckets". Often the data is stored in an array with each bucket being an index in the array.
Hashing Functions
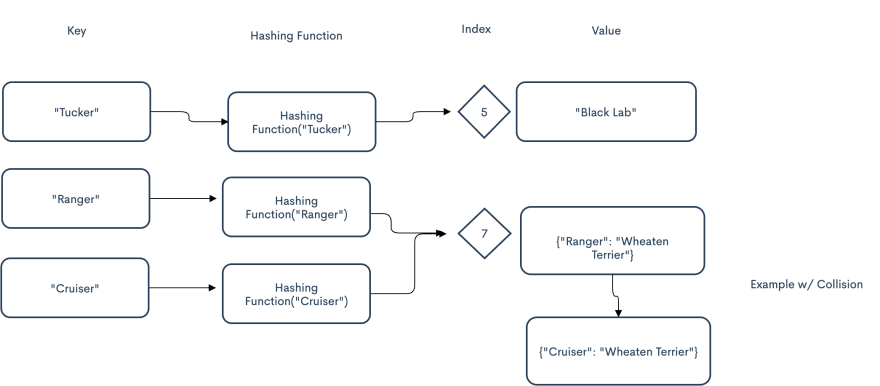
As I mentioned at the beginning of this blog, hash tables use a hashing function. This function tells us where to find an element in the array by inputting a key. Basically, the function will map a string to a number. Ideally, our hashing function will output unique index numbers for each key. Otherwise, the time complexity of retrieving an element will be closer to O(n) where n is the number of elements in the data set. When a hashing function returns the same outputted index for two or more different keys it is called a collision.
Collisions
Collisions happen when two keys get mapped to the same number or index. There are a few different ways to handle this scenario. One way is by storing the key value pairs that share the same index in a linked list. This is called separate chaining. Using this method, you will have to iterate through the pairs to find the item you are looking for. This could lead to inefficiency if there are a lot of collisions and bring the time complexity closer to O(n).
Here is an example with a collision. In this example the key is the name of the dog and the value is the dog's breed. We are hashing the dog's name to get the index we should store its data at. Cruiser and Ranger's names both hash to the index of 7, so they are stored in a linked list at index 7.
Another option to handle collisions is called open addressing, also known as closed hashing. With this method, the key is used to find the location in the array to look at first. If that spot is already full, a scheme will be used to probe the array for another location. This is done until an empty bucket is found to store the data. One scheme you can use is called linear probing where you look at the next spot in the array if the previous one is full. Here is a great Stack Overflow article on open addressing versus chaining.
Usually, open addressing is faster than separate chaining. However, if all of the buckets are close to being full, open addressing will be slow because it will take a lot of time to look through the buckets and find an open location.
Run Time
Hash tables perform fast retrieval, insertion, and deletion of data, however they are not very fast when the data needs to be searched / iterated over. For example, if you need to iterate over the data to find a maximum value, a hash table would not be the most efficient data structure.
Retrieval, insertion, and deletion from a hash table should have a time complexity of O(1), unless the hashing function isn't optimized and there are collisions. For example, if there are a lot of collisions and separate chaining is used, the lists will need to be iterated through in order to find the key value pair that you are looking for.
Closing Time
When is a time you have used hash tables in your applications? It would be great to hear some good use cases for this data structure.



Top comments (3)
That is a great question. I looked it up and this is what I found from this post:
"The term "hash" comes by way of analogy with its non-technical meaning, to "chop and mix". Indeed, typical hash functions, like the mod operation, "chop" the input domain into many sub-domains that get "mixed" into the output range to improve the uniformity of the key distribution."
Hash tables are so prevalent in programming languages that you may not realize you are using one behind the scenes, in the implementation of your favorite data structure. Thanks, Rachel, for shining light on a frequently overlooked area.
Thank you for commenting Eric!