Intro to Binary Search

#javascript #computerscience #beginners

Quick Overview

Binary search is an important searching algorithm to learn for technical interviews and for use in searching problems you might encounter in your projects. For large arrays this algorithm is very quick. The only catch is that it can only be done with sorted arrays.

The Phone Book Analogy

A lot of people like to think of searching through a phone book when they think about binary search. This analogy is a little bit antiquated considering most people just search the contacts in their phones these days, however I think it's a good way to understand the concept.

If you were to look up a last name in the phone book, let's say the name Smith, how would you go about doing this? Most people would first flip to where they thought the name might be, which might be a little past halfway. Then they would check the names on the page they flipped to. Let's say you flipped to a page with last names starting with P. You would know that since P comes before S, you need to now check the back-half of the phone book. Therefore, you can eliminate all of the names in the phone book from the beginning until just past the page you are on, since you know Smith isn't on that page.

You would repeat this process, searching a spot roughly halfway through the remainder of the phone book and comparing the names to your target name, Smith, until you found the page with the name you are searching for.

This is very similar to how binary search works and explains why it's so much faster than searching each element one by one. Since the data is sorted, we can take a better guess as to where our target value is.

Working on the Pseudocode

With this knowledge of the algorithm, we can begin to work on some pseudocode for how our algorithm should work. Let's say we are looking for the target value 5 in the array: [0, 1, 2, 3, 5, 7, 8].

We know that our function should take two parameters, a sorted array and a target value to find in the array. We know we will be looking at the element in the middle of the array each time and comparing that to our target. If we don't find a match, we know we will need to look at a new part of the array, either the portion after the middle or before the middle.

One good way to find the middle of the array is by using the average. To find the average, we know we will need pointers to the left and right sides of the portion of the array that we are currently "investigating." We will need to add the pointers together and divide them by two. Since this is the case, we will store the index at the farthest left side of the portion of the array we are looking at, as well as the index of the farthest right position.

Next we will create a loop so that we can continue looking at different portions of the array until we find the match. With each loop, we will calculate the index at the middle of the portion of the array we are looking at and compare the value at that index to our target value. If the middle value matches our target, we will return the index of the middle value. If the middle value is less than our target, we will set our left pointer to one above our current middle to look at the last half of the current scope of the array. If the middle value is greater than our target, we will set the right pointer to one below the middle index to look at the first half of the current scope of the array. We will then execute the loop again.

If we can't find a match after searching the entire array, then we will want to return -1, indicating no index found for the target value.

Here is some pseudocode for what we have so far:

function binarySearch(sortedArray, targetValue) {
  //set leftSide to beginning of array at first
  let leftSide = 0
  //set rightSide to end of array at first so the entire array is in scope
  let rightSide = endOfArray

  while (targetNotFound) {
    // average the left and right pointer to find middle. Will need to round this number to get an integer
    let middle = average(left, right)

    if (targetValue === valueAtMiddleIndex) {
      return middle
    } else if (valueAtMiddleIndex < targetValue) {
      leftSide = middle + 1
    } else if (valueAtMiddleIndex > targetValue) {
      rightSide = middle - 1
    }
  }
  // if target value can't be found in array
  return -1
}

Let's walk through the code with our test case.

We start with [0, 1, 2, 3, 5, 7, 8] and are searching for 5
leftSide will be initialized at 0. rightSide will be initalized at 6.
1st loop:
- middle initialized at 3
- The element at index 3 is 3
- Does 3 === 5? No, it is smaller than the target.
- leftSide now = 3 + 1 = 4
2nd loop:
- We are now looking at this portion of the array: [5, 7, 8]
- middle now = (4 + 6) / 2 = 5
- The element at index 5 is 7
- Does 7 === 5? No, it is bigger than the target.
- rightSide now = 5 -1 = 4
3rd loop:
- Now we are only looking at this portion: [5]
- middle now = (4 + 4) / 2 = 4
- The element at index 4 is 5
- Does 5 === 5. Yes!
- Return middle which = 4

It works!

A Problem

Do you see a problem with the pseudocode?

If you thought that the loop could execute forever in certain cases, you would be right. With our current code, we only stop the loop if we find the target value, however if we never find it the loop will continue forever.

A good way to short circuit this loop would be to make sure the left pointer never goes past the right. That is, if the array is down to one more value to check and that value is not equal to our target, we exit the loop. Here is our updated pseudocode:

function binarySearch(sortedArray, targetValue) {
  //set leftSide to beginning of array at first
  let leftSide = 0
  //set rightSide to end of array at first so the entire array is in scope
  let rightSide = endOfArray

  // exit loop if left pointer goes past rightPointer. I removed the targetNotFound condition since the return statement within the loop already handles this.
  while (leftSide <= rightSide) {
    // average the left and right pointer to find middle. Will need to round this number to get an integer
    let middle = average(left, right)

    if (targetValue === valueAtMiddleIndex) {
      return middle
    } else if (valueAtMiddleIndex < targetValue) {
      leftSide = middle + 1
    } else if (valueAtMiddleIndex > targetValue) {
      rightSide = middle - 1
    }
  }
  // if target value can't be found in array
  return -1
}

Let's walk through the pseudocode using the same array as before with a new target value of 4.

We start with [0, 1, 2, 3, 5, 7, 8] and are searching for 4
leftSide will be initialized at 0. rightSide will be initalized at 6.
1st loop because leftSide(0) <= rightSide(6):
- middle initialized at 3
- The element at index 3 is 3
- Does 3 === 4? No, it is smaller than the target.
- leftSide now = 3 + 1 = 4
2nd loop because leftSide(4) <= rightSide(6):
- We are now looking at this portion of the array: [5, 7, 8]
- middle now = (4 + 6) / 2 = 5
- The element at index 5 is 7
- Does 7 === 4? No, it is bigger than the target.
- rightSide now = 5 - 1 = 4
3rd loop because leftSide(4) <= rightSide(4):
- Now we are only looking at this portion: [5]
- middle now = (4 + 4) / 2 = 4
- The element at index 4 is 5
- Does 5 === 4. No, it is bigger than the target.
- rightSide now = 4 - 1 = 3
Exit while loop because leftSide(4) is NOT <= rightSide(3)
Return -1

It works!

This pseudocode is already pretty close to the real thing, but I challenge you to get a working JavaScript function yourself before continuing on. Here's a gif so you don't sneak a peek at my code below.

My Implementation of Binary Search

Here is my implementation of this algorithm using JavaScript:

function binarySearch(sortedArr, value){
  let left = 0;
  let right = sortedArr.length - 1;

  // I chose to initialize these variables outside the loop
  let middle;
  // currentElem will be the element that is at the middle index
  let currentElem;

  while (right >= left) {
      // Math.floor() will round the decimal down to the nearest integer
      middle = Math.floor((left + right) / 2)

      currentElem = sortedArr[middle];

      if (currentElem === value) {
          return middle;
      } else if (currentElem < value) {
          left = middle + 1;
      } else if (currentElem > value) {
          right = middle - 1;
      }
  }
  return -1;
}

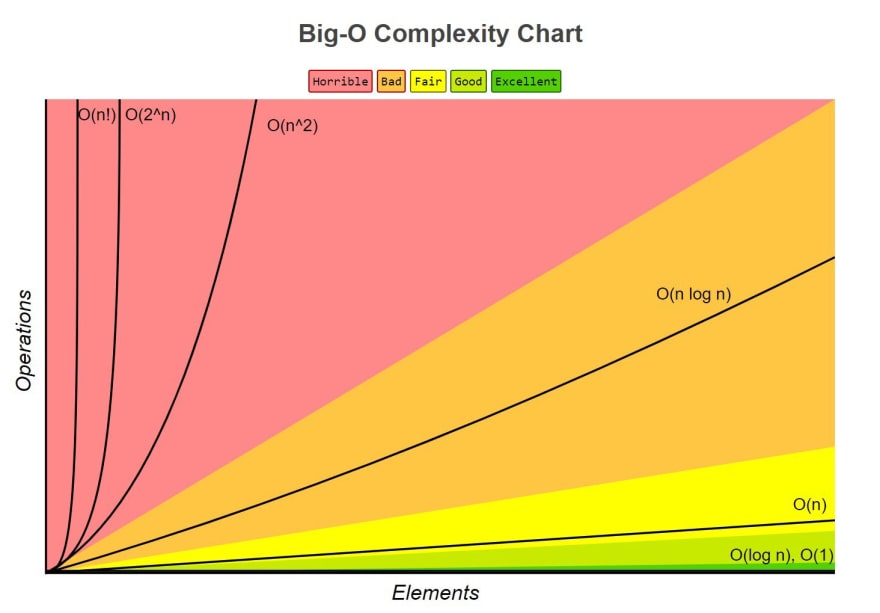
Big O of Binary Search

The worst case performance of Big O is O(log n) which is very fast. For perspective, most of JavaScript's built in searching methods, such as Array.prototype.includes(), have a time complexity of O(n) because they use linear search.

Binary search is significantly faster than linear search for arrays that aren't considered small. If the array is small, it might not perform faster than linear search. The only downside with binary search that I see is that the data must be sorted.

Cheers

Thank you for reading. I hope I could teach you something new today and I hope everyone is having a fun and safe weekend!

Resources

Top comments (6)

Tomasz Gieorgijewski • Apr 19 '20

Good job! Have you tried recursion version of binary search?
Yeah, data must be sorted, so if you don't know the data you will have to sort it anyway yourself which get it down to O(n log n). So simple linear search would be good enough then.