Day 11 - Merge Sorted Array

The Problem

Given two sorted integer arrays nums1 and nums2, merge nums2 into nums1 as one sorted array.

The number of elements initialized in nums1 and nums2 are m and n respectively. You may assume that nums1 has enough space (size that is equal to m + n) to hold additional elements from nums2.

Example 1:

Input: nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
Output: [1,2,2,3,5,6]

Example 2:

Input: nums1 = [1], m = 1, nums2 = [], n = 0
Output: [1]

Constraints:

• 0 <= n, m <= 200
• 1 <= n + m <= 200
• nums1.length == m + n
• nums2.length == n
• -109 <= nums1[i], nums2[i] <= 109

My Tests

Link to code

import pytest
from .Day11 import Solution

s = Solution()


@pytest.mark.parametrize(
    "nums1,m,nums2,n,expected",
    [
        ([1, 2, 3, 0, 0, 0], 3, [2, 5, 6], 3, [1, 2, 2, 3, 5, 6]),
        ([1], 1, [], 0, [1]),
        ([0], 0, [1], 1, [1]),
    ],
)
def test_merge(nums1, m, nums2, n, expected):
    s.merge(nums1, m, nums2, n)
    assert nums1 == expected

My Solution

Link to code

from typing import List


class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        i = len(nums1) - 1

        while m >= 1 and n >= 1:
            if nums1[m - 1] < nums2[n - 1]:
                nums1[i] = nums2[n - 1]
                n -= 1
            else:
                nums1[i] = nums1[m - 1]
                m -= 1
            i -= 1

        nums1[:n] = nums2[:n]

Analysis

My Commentary

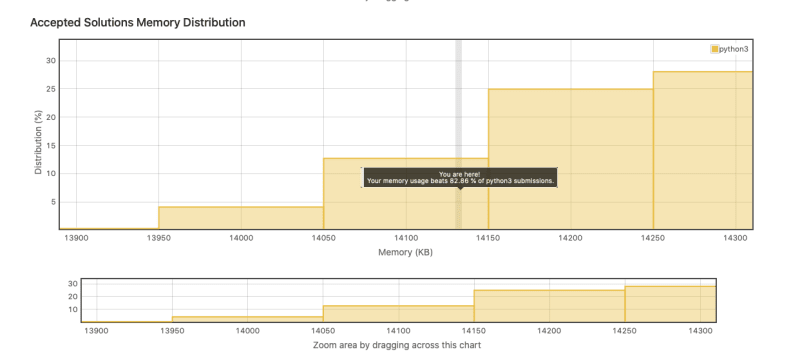
This one was straightforward enough. The fact that we are supplied n and m is a hint that we need to do more than simply merge the 2 lists to get an optimal solution.

Because we know the lists are sorted we can use that to do this all in one pass and in place. Starting at the end of each list (then end of nums1 is n -1 even though len(num1) == n + m. Then we take the largest number and put it in the buffer space of nums1 which we index with i starting at len(nums1) - 1.

The very last step is to fill out nums1 with any values we didn't catch from nums2.