hi👋Devs,
In the previous one we have learned about the Merge Sort algorithm and in this article, we will discuss the QuickSort algorithm, how its work, time & space complexities and pros & cons.
Quick Sort
Quick Sort algorithm is an in-place sorting algorithm means this algo doesn't require any extra space except temp variables, to perform sorting.
This algo is also based on the divide and conquer approach.
lets understand how quick sort work.
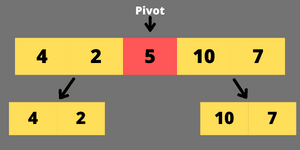
step-1 select a pivot element.
you can choose any element as a pivot from the array
- first element
- last element
- any random element
lets say i choose the first element of the array as pivot
step-2 place the pivot element in its right position.
now in this step we have to place the pivot element to its right position but we have to rearrange the array in such a way that
- put all smaller elements (which are less than pivot) before pivot element.
- put all greater elements (which are greater than pivot) after the pivot element.
we also called this step as a partition logic.
step-3 divide the array into sub-array.
divide the array into the left sub-array and sub-right array based on the pivot point and apply the same approach for the sub-arrays until sub array size becomes 1
implementation
now understand how we can implement this algo pragmatically
Pseudocode for quickSort( arr, start, end)
1. find the pivot index pivotIndex by using partition logic.
pivotIndex = partition( arr, start, end)
2. divide the array into sub-arrays using pivotIndex.
quickSort(arr, start, point-1)
quickSort(arr, point+1, end)
3. repeat these steps until the sub-array size becomes 1.
Pseudocode for partition( arr, start, end)
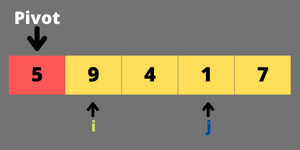
step-1 make first element as pivot.
pivot = arr[first]
step-2 run a loop while start < end and then,
1. initialise
i&jvariables.
i = start
j = end
2. linearly increase the
iwhilepivot > arr[i]3. linearly decrease the
jwhilepivot < arr[j]
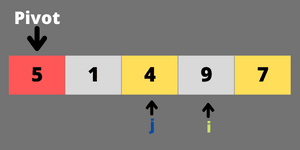
4. swap
ithelement withjthelement ,ifi < j
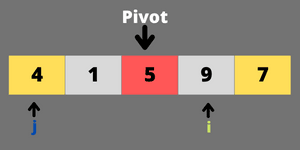
step-3 swap pivot element with jth element.
step-4 return the right pivot index position j
Time & Space Complexity
in average case the time complexity will be nLogn.
this algo does not require any extra space so , the space complexity is O(1).
Pros & Cons
- it does not require extra memory.
- pretty fast & efficient in most cases.
- the worst-case complexity is
n^2. - use recursion.
Java Implementation
import java.util.Arrays;
class Main{
public static void main(String[] args){
int[] arr = new int[] {3,12,90,2,5,16,25,44,70,0};
System.out.println("unsorted array: "+Arrays.toString(arr));
qSort(arr,0,9);
System.out.println("sorted array: "+Arrays.toString(arr));
}
private static void qSort(int[] arr,int start,int end){
if(start < end){
int p = partition(arr,start,end);
qSort(arr,start,p-1);
qSort(arr,p+1,end);
}
}
private static int partition(int[] arr,int s,int e){
int pivot = arr[s];
int i = s;
int j = e;
while(i < j){
while(arr[i]<=pivot && i<e) i++;
while( arr[j]>pivot && j>s ) j--;
if(i < j)
swap(arr,i,j);
}
swap(arr,s,j);
return j;
}
private static void swap(int[] arr,int i, int j){
int t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
}
Thank you for reading this article. save it and share it with your dev friends. if you find any errors let me know in the comment section.










Top comments (0)