Convolutional Neural Networks are a part of what made Deep Learning reach the headlines so often in the last decade. Today we'll train an image classifier to tell us whether an image contains a dog or a cat, using TensorFlow's eager API.
Artificial Neural Networks have disrupted several industries lately, due to their unprecedented capabilities in many areas. However, Different Deep Learning architectures excel on each one:
- Image Classification (Convolutional Neural Networks).
- Image, audio and text generation (GANs, RNNs).
- Time Series Forecasting (RNNs, LSTM).
- Recommendations Systems.
- A huge et cetera (e.g., regression).
Today we’ll focus on the first item of the list, though each of those deserves an article of its own.
What are Convolutional Neural Networks?
In MultiLayer Perceptrons (MLP), the vanilla Neural Networks, each layer’s neurons connect to all the neurons in the next layer. We call this type of layers fully connected.
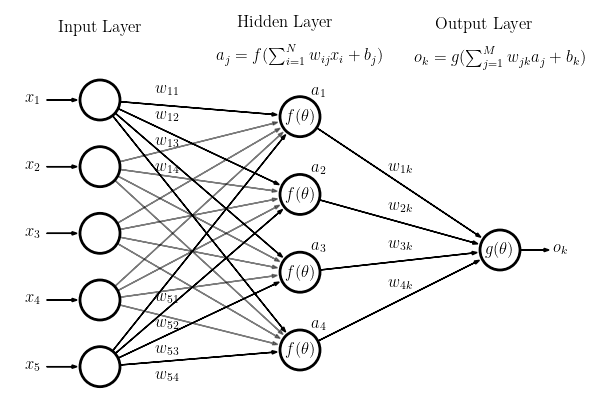
A Convolutional Neural Network is different: they have Convolutional Layers.
On a fully connected layer, each neuron’s output will be a linear transformation of the previous layer, composed with a non-linear activation function (e.g., ReLu or Sigmoid).
Conversely, the output of each neuron in a Convolutional Layer is only a function of a (typically small) subset of the previous layer’s neurons.

Outputs on a Convolutional Layer will be the result of applying a convolution to a subset of the previous layer’s neurons, and then an activation function.
What is a convolution?
The convolution operation, given an input matrix A (usually the previous layer’s values) and a (typically much smaller) weight matrix called a kernel or filter K, will output a new matrix B.

if K is a CxC matrix, the first element in B will be the result of:
- Taking the first CxC submatrix of A.
- Multiplying each of its elements by its corresponding weight in K.
- Adding all the products.
These two last steps are equivalent to flattening both A's submatrix and K, and computing the dot product of the resulting vectors.
We then slide K to the right to get the next element, and so on, repeating this process for each of A‘s rows.

Depending on what we want, we could only start with our kernel centered at the Cth row and column, to avoid “going out of bounds”, or assume all elements “outside A” have a certain default value (typically 0) –This will define whether B‘s size is smaller than A‘s or the same.
As you can see, if A was an NxM matrix, now each neuron’s value in B won’t depend on N*M weights, but only on C*C (much less) of them. This makes a convolutional layer much lighter than a fully connected one, helping convolutional models learn a lot faster.
Granted, we will end up using many kernels on each layer (getting a stack of matrices as each layer’s output). However, that will still require a lot less weights than our good old MLP.
Why does this work?
Why can we ignore how each neuron affects most of the others? Well, this whole system holds up on the premise that each neuron is strongly affected by its “neighbors”. Faraway neurons, however, have only a small bearing on it.
This assumption is intuitively true in images –if we think of the input layer, each neuron will be a pixel or a pixel’s RGB value. And that’s part of the reason why this approach works so well for image classification.
For example, if I take a region of a picture where there’s a blue sky, it’s likely that nearby regions will show the sky as well, using similar tones.
A pixel’s neighbors will usually have similar RGB values to it. If they don’t, then that probably means we are on the edge of a figure or object.
If you do some convolutions with pen and paper (or a calculator), you’ll realize certain kernels will increase an input’s intensity if it’s on a certain kind of edge. In other edges, they could decrease it.
As an example, let’s consider the following kernels V and H:

V filters vertical edges (where colors above are very different from colors below), whereas H filters horizontal edges. Notice how one is the transposed version of the other.
Convolutions by example
Here’s an unfiltered picture of a litter of kittens:
Here’s what happens if we apply the horizontal and vertical edge filters, respectively:
We can see how some features become a lot more noticeable, whereas others fade away. Interestingly, each filter showcases different features.
This is how Convolutional Neural Networks learn to identify features in an image. Letting it fit its own kernel weights is a lot easier than any manual approach. Imagine trying to figure out how you should express the relationship between pixels… by hand!
To really grasp what each convolution does to a picture, I strongly recommend you play around on this website. It helped me more than any book or tutorial could. Go ahead, bookmark it. It’s fun.
Alright, you’ve learned some theory already. Now let’s move on to the practical part.
How do you train a Convolutional Neural Network in TensorFlow?
TensorFlow is Python’s most popular Deep Learning framework. I’ve heard good things about PyTorch too, though I’ve never had the chance to try it.
I’ve already written one tutorial on how to train a Neural Network with TensorFlow’s Eager API, focusing on AutoEncoders.
Today will be different: we will try three different architectures, and see which one does better. As usual, all the code is available on GitHub, so you can try everything out for yourself or follow along. Of course I’ll also be showing you Python snippets.
The Dataset
We will be training a neural network to predict whether an image contains a dog or a cat. To do this we’ll use Kaggle’s cats and dogs Dataset. It contains 12500 pictures of cats and 12500 of dogs, with different resolutions.
Loading and Preprocessing our Image Data with NumPy
A neural network receives a features vector or matrix as an input, typically with fixed dimensions. How do we generate that from our pictures?
Lucky for us, Python’s Image library provides us an easy way to load an image as a NumPy array. A HeightxWidth matrix of RGB values.
We already did that on this article, so I’ll just reuse that code.
However we still have to fix the fixed dimensions part: which dimensions do we choose for our input layer? This is important, since we will have to resize every picture to the chosen resolution. We do not want to distort aspect ratios too much in case it brings too much noise for the network.
Here’s how we can see what the most common shape is in our dataset.
I sampled the first 1000 pictures for this, though the result did not change when I looked at 5000. The most common shape was 375×500, though I decided to divide that by 4 for our network’s input.
This is what our image loading code looks like now.
Finally, you can load the data with this snippet. I chose to use a sample of 4096 pictures for the training set and 1024 for validation. However, that’s just because my PC couldn’t handle much more due to RAM size.
Feel free to increase these numbers to the max (like 10K for training and 2500 for validation) if you try this at home!
Training our Neural Networks
First of all, as a sort of baseline, let’s see how good a normal MLP does on this task. If Convolutional Neural Networks are so revolutionary, I’d expect the results to be terrible for this experiment.
So here’s a single hidden layer fully connected neural network.
All the trainings for this article were made using AdamOptimizer, since it’s the fastest one. I only tuned the learning rate per model (here it was 1e-5).
I trained this model for 10 epochs, and it basically converged to random guessing. I made sure to shuffle the training data, since I loaded it in order and that could’ve biased the model.
I used MSE as loss function, since it’s usually more intuitive to interpret. If your MSE is 0.5 in binary classification, you’re as good as always predicting 0. However, MLPs with more layers, or different loss functions did not perform better.
Training a Convolutional Neural Network
How much good can a single convolutional layer do? Let’s see.
For this network, I decided to add a single convolutional layer (with 24 kernels), followed by 2 fully connected layers.
All Max Pooling does is reduce every four neurons to a single one, with the highest value between the four.
After only 5 epochs, it was already performing much better than the previous networks. With a validation MSE of 0.36, it was a lot better than random guessing already. Notice however that I had to use a much smaller learning rate. Also, even though it learned in less epochs, each epoch took much longer. The model is also quite a lot heavier (200+ MB).
I decided to also start measuring the Pearson correlation between predictions and validation labels. This model scored a 15.2%.
Neural Network with two Convolutional Layers
Since that model had done so much better, I decided I would try out a bigger one. I added another convolutional layer, and made both a lot bigger (48 kernels each). This means the model gets to learn more complex features from the images. However it also predictably meant my RAM almost exploded. Also, training took a lot longer (half an hour for 15 epochs).
Results were superb. The Pearson correlation coefficient between predictions and labels reached 0.21, with validation MSE reaching as low as 0.33.
Let’s measure the network’s accuracy. Since 1 is a cat and 0 is a dog, I could say “If the model predicts a value higher than some threshold t, then predict cat. Else predict dog.” After trying 10 straightforward thresholds, this network had a maximum accuracy of 61%.
Even bigger Convolutional Neural Network
Since clearly adding size to the model made it learn better, I tried making both convolutional layers a lot bigger, with 128 filters each. I left the rest of the model untouched, and didn’t change the learning rate.
This model finally reached a correlation of 30%! Its best accuracy was 67%, which means it was right two thirds of the time. I assume an even bigger model could’ve fit the data even better. However, this one was taking 7 minutes per epoch already, and I didn’t want to leave the next one training all morning.
Usually, there’s a tradeoff to be made between a model’s size, and time constraints. Size limits how well the network can fit the data (a small model will underfit ), however I won’t wait 3 hours for my model to learn.
The same concerns may apply if you have a business deadline.
Conclusions
We’ve seen Convolutional Neural Networks are significantly better than vanilla architectures at image classification tasks. We also tried different metrics to measure model performance (correlation, accuracy).
We learned about the tradeoff between a model’s size (which prevents underfitting) and its convergence speed.
Lastly, we used TensorFlow’s eager API to easily train a Deep Neural Network, and numpy for (albeit simple) image preprocessing.
For future articles, I believe we could experiment a lot more with different pooling layers, filter sizes, striding and a different preprocessing for this same task.
Did you find this article useful? Would you have preferred to learn more about anything else? Is anything not clear enough? Let me know in the comments!
Find me on Twitter, Medium or Dev.to if you have any questions, or want to contact me for anything. If you want to start a career in Machine Learning, here’s my recommended reading list.





Top comments (0)