What is a Graph data structure?
A Graph is a collection of vertices/nodes and edges in a way that vertices/nodes are connected by an edge.
Graph Terminologies
Vertex or Node
Every individual point that holds or represents some kind of data is called vertex or node.
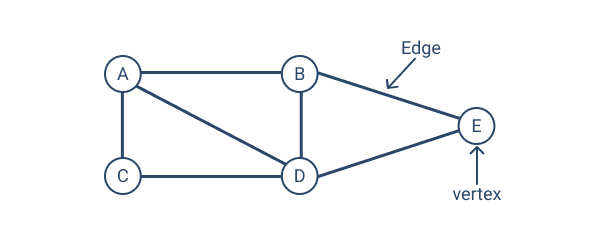
In fig01 points "A", "B", "C", "D", "E" are vertex/node since there multiple vertex/node so it called vertices/nodes.
nodes and vertices both terms are the same.
Edge
A connection between two nodes is called an edge. In fig01 the connection between node B and node E is edge similarly A-B, A-C, A-C, A-D, B-D, C-D, D-E are edges.
Adjacent
This terminology often used with vertices/nodes.
Adjacent node shares a common edge.
let me explain you.
In fig02 nodes B, D, C shares a common edge with node "A" and similarly with others too.
Now if i ask you what are adjacents nodes of "A" that means all the nodes that share common edges with node "A".
Adjacent of all nodes
| Nodes | Adjacents |
|---|---|
| A | BDC |
| B | ADE |
| C | AD |
| D | CABE |
| E | BD |
Degree
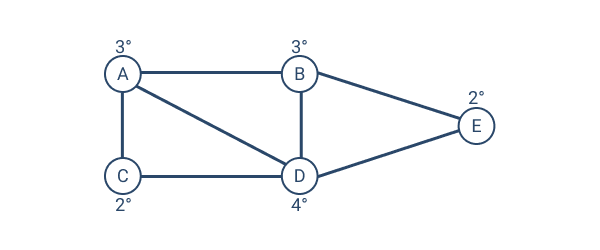
The degree is the number of edges connected to a node.
for example, the node "D" has a degree of 4 while the "E" has a degree of 2.
Types of graph
disconnected graph
In a disconnected graph, not all nodes have edges. nodes might be isolated.
if you see the above disconnected graph, there are three isolated regions. in simple words, these three regions don't have a connection between them.
connected graph
a graph is connected if all nodes have at least one edge.
undirected graph
an undirected graph has no direction. The edges indicate a two-way relationship, in that each edge can be traversed in both directions.
directed graph
a directed graph has edges with direction. The edges indicate a one-way relationship, in that each edge can only be traversed in a single direction.
complete graph
A graph is said to be complete if each node have a degree of n-1(n = total nodes)
sound like mathematics
in simple words
A graph is said to be complete if each node has an edge with all other nodes except itself.
cyclic graph
A graph can have cycles which means that if you traverse through the node, you could get the same node more than once.
acyclic graph
a graph is acyclic that means the graph must have at least one node with no targets (called a leaf).
in the above image, the orange node doesn't have any outgoing edge.
Applications Of Graph
- Social media like Facebook, LinkedIn uses graphs that store users, groups, check-ins, likes and more as nodes.
- Google Maps, Apple Maps, Waze use graphs to treat all cities and places as nodes and routes between them as edges.
- Webgraph describes a directed graph between pages of the WWW. Each page is a vertex and the hyperlinks are edges. This is the basic idea behind the Google Page Ranking Algorithm.
- Uber, Ola, Lyft uses a graph to find the shortest and cheapest path for a car from one city to another.
- The graph also used in a database for representing Entity-Relationship.
- Graph theory also used to study molecules in chemistry and physics.
reference
this tutorial first published on codebond.co




Top comments (0)