Introduction
In previous tutorials, we learned some basics of a graph, it's representation, and it's application. In this tutorial, we are going to practically implement our previous knowledge and learn to create an undirected graph.
pre-requisite:
class Graph {
constructor(){
this.nodes = new Map()
}
addNode(){}
addEdge(){}
removeNode(){}
removeEdge(){}
depthfirstSearch(){}
breadthFirstSearch(){}
display(){}
}
The above snippet shows the steps and method takes to create a graph. as we go further, we will get to see the implementation and pseudo-code.
let's start
this.nodes
this.nodes is an Object in which key holds the node and value hold an array of adjacent nodes.
initially, it is empty.
this.nodes = {}
addNode(node)
It adds a new node to the graph.
addNode(node){
this.nodes.set(node,[])
}
the array of adjacent nodes is initially set to be empty because the new node does not have any edge yet.
addEdge(source,destination)
It adds an edge between source node and destination node.
In order to add an edge, we need the adjacency list of the source node then push destination node to it. since it is an undirected graph, we also need to push the source node to the adjacency list of destination node.
addEdge(source,destination){
this.nodes.get(source).push(destination)
this.nodes.get(destination).push(source)
}
let's implement what we learn so far.
removeNode(node)
It basically removes the node from the graph.
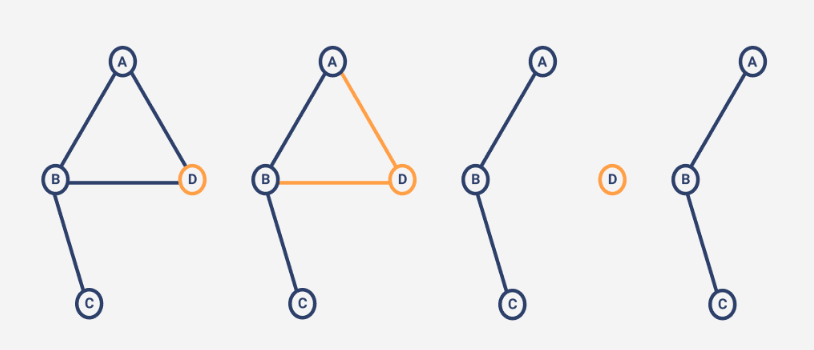
But, in order to remove a node, we must first remove the edges that are associated with the removal node.
In the above example. to remove node "D" we first have to remove the edges that are associated with "D" which are "D-A" and "D-B" after that we can remove the "D".
In the following code, we added a helper function getIndexAndRemoveItem(item,list) it takes argument item as node (that we are going to remove) and list as an array (from which we are going to remove item).
removeNode(node) {
let neighbors = this.nodes.get(node);
for(let neighbor of neighbors){
let adjacencyListOfNeighbor = this.nodes.get(neighbor);
this.getIndexAndRemoveItem(node, adjacencyListOfNeighbor);
}
this.nodes.delete(node);
}
getIndexAndRemoveItem(item, list) {
const index = list.indexOf(item);
list.splice(index, 1);
}
Checkout the 👉 pseudocode for removeNode()
removeEdge(source,destination)
It removes the edge between source node and destination node.
To remove the edge, we must have all the nodes that share an edge with source node in a simple term adjacency list of the source node. since it is an undirected graph, we need an adjacency list of destination node as well.
Then, with the help of our helper function getIndexAndRemoveItem() we can remove the edge.
removeEdge(source, destination) {
let adjacencyListOfSource = this.nodes.get(source);
let adjacencyListOfDestination = this.nodes.get(destination);
this.getIndexAndRemoveItem(source, adjacencyListOfDestination);
this.getIndexAndRemoveItem(destination, adjacencyListOfSource);
}
getIndexAndRemoveItem(item, list) {
const index = list.indexOf(item);
list.splice(index, 1);
}
Checkout the 👉 pseudocode for removeEdge()
let's implement
depthFirstSearch(startingNode)
depth-first-search is a traversal technique in which we go as deep as possible in the graph once we reach a node where we cannot further go down, we backtrack to the node we came from. This process repeated until we explore all other nodes in the graph.
depthFirstSearch(startingNode) {
let visitedNode = [];
this.dfsRecursion(startingNode, visitedNode);
}
dfsRecursion(currentNode, visitedNode) {
visitedNode[currentNode] = true;
console.log(currentNode);
let adjacencyListOfCurrentNode = this.nodes.get(currentNode);
for (var node of adjacencyListOfCurrentNode) {
if (!visitedNode[node]) this.dfsRecursion(node, visitedNode);
}
}
checkout the 👉 pseudocode for depthFirstSearch()
breadthFirstSearch(startingNode)
Unlike depth-first-search, where we go deep before exploring neighbors, in breadth-first-search, we explore all the neighbors of a node before moving a level down.
breadthFirstSearch(startingNode) {
let visitedNode = [];
let queue = [];
visitedNode[startingNode] = true;
queue.push(startingNode);
while (queue.length > 0) {
const currentNode = queue.shift();
console.log(currentNode);
const adjacencyListOfCurrentNode = this.nodes.get(currentNode);
for (let node of adjacencyListOfCurrentNode) {
if (!visitedNode[node]) {
visitedNode[node] = true;
queue.push(node);
}
}
}
}
checkout the 👉 pseudocode for breadthFirstSearch()
Summary
We learned to create and manipulate a graph by adding, removing nodes and edges. we also covered the depth-first-search and breadth-first-search algorithm.
Soon in the next posts, we will see the more efficient and professional way to create a graph.
Thank for reading 🙏
Was this article helpful? don't forget to share because Sharing is Caring.





Top comments (0)