Natural Search Algorithm

This post is about function I wrote while solving LeetCode task.

Complexity of naive solution for this task is O(w²) where w is weights size.
But it can be done better with little improvement.
Instead checking every possible day from 1 to weights.length we can implement natural search algorithm and finish this task with O(w * log(w)) complexity.

Here is code I wrote:
https://github.com/gkucmierz/algorithms/blob/master/js/natural_search.js

Using this function is very simple.
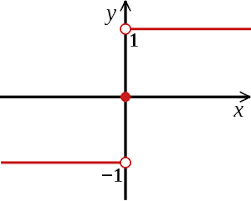
Whenever we have Signum function with unknown bias.

Like this:

const fn = n => Math.sign(n - 345) >= 0;

345 here is random unknown number.
We can easily find it using simple code:

const fn = n => Math.sign(n - 345) >= 0;

console.log(naturalSearch(fn));

Second parameter for naturalSearch function which is retFirstTrue indicates if function should return first natural number when condition is returning true value, or last natural number when it is still false.

Lets check if algorithm really is calling function optimal number of times:

const fn = n => {
  const res = n >= 345;
  console.log('checking number:', n, 'result:', res);
  return res;
};

console.log(naturalSearch(fn));

Than we have this result:

'checking number:', 1, 'result:', false
'checking number:', 2, 'result:', false
'checking number:', 4, 'result:', false
'checking number:', 8, 'result:', false
'checking number:', 16, 'result:', false
'checking number:', 32, 'result:', false
'checking number:', 64, 'result:', false
'checking number:', 128, 'result:', false
'checking number:', 256, 'result:', false
'checking number:', 512, 'result:', true
'checking number:', 384, 'result:', true
'checking number:', 320, 'result:', false
'checking number:', 352, 'result:', true
'checking number:', 336, 'result:', false
'checking number:', 344, 'result:', false
'checking number:', 348, 'result:', true
'checking number:', 346, 'result:', true
'checking number:', 345, 'result:', true
345

As we can see in first phase algorithm is trying to find true value by multiplying number by 2, then when it find, it can find exact point using bisection technique.