Linear data structures is one of the most used DSs in programming it has many different Data structures like arrays linked-lists stack …etc , in this article we will talk about this tow DS arrays and Linked-list ,they are so important and basically every programmer should know about this tow even if he’s is just starting his career he will find arrays and linked lists in the first topic that he will learn due to there importance as a way of storing and manipulating data in a lot of problems.
Arrays (static arrays and dynamic arrays):
Static arrays :
a static Array is a static data structures that allow you to store any type of data as long as the length of the array is specified at the creation of it, this length can’t be changes since it’s a static DS . Each value in an array has an index that refers to it and gives the programmer a way to access it’s value knowing that the indexes start from 0 to n as an example: the first element of an array of integers will be : integerTable0, the type of data stored in the array in most languages has to be the same type for all values. (ex: all integers or all string , not a few of integers and some other data types).
when you should use static arrays ?
- when you know the max length of your array.
- most of the time static arrays are used as temporary memory to store objects.
- used to return multiple values from a function.
- used as buffers for input and output.
- used to store results of the sub solutions like in dynamic programming.
Dynamic arrays :
a dynamic array is an array that has no limit to the number of value that you can put in and has the same operation that you can apply to a normal static array.
when you should use dynamic arrays ?
basically when you don’t know how much data you need to store.
How you can implement a dynamic array ?
The code source for the dynamic array is in this file :
https://github.com/GourineAyoubPrf/ArrayAndLinkedLists/tree/main/src/arraysandlinkedlistes
one of the ways to make a dynamic arrays is to use static arrays like this :
- at first we have a table of length 1
- each time the user want to add an element to the dynamic array we test the length of the initial array
- if there is place to add : add the element normally in the next index.
- if the size is not enough then:
- create a new array that has a double size of the previous one.
- copy all the element from the previous array to the new .
- add the new element to the new array .
- and finally the new array becomes our initial array and we repeat this process each time when there is no enough space to add.

- in case of the deletion :
- create a new array with the size of number Of elements in our initial array -1.
- copy all the elements except the element that we want to delete.
- the new array becomes our initial array.

this data structures are already implemented in the >programming languages but to understand them more and get >good in working with theme you need to understand how they >are implemented and how they work.
the implementation is different from one language to >another some operation are allowed in one language and not >in another but now that you know how things works if >something is not good for you you can implement your own >data structure and make the operations that you want for it.
in java we use this sign example : in the >class declaration so we can use the generic types in our >array implementation so it supports all data types. and we >implement the iterator interface in case you want to use >iterator to loop over the elements.
Array Operations :
arrays as a data structures has many operations that can be applied to. We have basic operations like :
- search
- add
- access element
- remove element. and some more complicated and specified operations like :
- remove element at index / remove the first/ remove the last.
- sort the elements.
- invert the table elements
- shift elements
- … etc.
Array operations complexity :
The complexity is different from the static array to dynamic array , and also it can be different in one language to another due to the way of implementation but generally this is it :
we are talking about worst case here because there is some >search methods that can take less time if the array is >ordered (we will talk about searching and sorting methods in >another article).
How arrays are sorted in the memory ?
Arrays are stored in a contiguous space in memory as an example if you have an array of length 10 the compiler will have to find 10 successive places in the memory to store the data (places mean the pace necessary for storing one element of the specified type) , this behavior is only with arrays since it uses indexes so the memory address has to be side to side but it’s different with other DS like linked list (will discus later).
Why indexes start from 0 in arrays ?
a little story :
- At the first creation of arrays in the programming world the address of the array was set to be the address of the first element of that array so they are the same address in the memory , as an example if we have an array of integers named myArray with this values [5,2,6,8,91,100,235] if we say that the address of the first value “5” that we access it like this myArray[0] is the address named 111 (just a a naming ) then the address that reference to the array it self is 111 and when the programmers implemented the arrays (low level implementation) to access an array value they did this operation as example : myArray[5] for the compiler to know it’s place he must do this operation :
- the address of myArray[5] = the address of MyArray + 5 so the address will be 111 + 5 = 116 then he will go to the memory the address 116 an read it value and give it to you as the value of myArray[5] in our case it will be 100. now after you know that imagine that we start from 1 and not 0 and we want to access the value of myArray[1] the compiler have to find the address so 111 + 1 = 112 but the address 112 contains 2 not 5 which is wrong because our first element is 5 and the compiler need each time to do -1 after the sum sow he can get the write result and this will be not good for the performance because we are talking about low level implementation , for that the element’s start from 0 and not from 1.
to be more clear the address of the element that we try to access is calculated with this formula :
address of accessed element = address of the array + index * >(size of one element of the type that the arrays contain).
Example : if we say an integer take a size of 5 to store one >element then :
address of accessed element = address of the array+ index * >5 (because each integer take a size of 5 in the memory) , >Because each case has a size fit for one element of the >declared type.
If you want to learn more about this you can search about >heap memory and memory management in the operating systems .
Linked list (single linked list, double linked list and circular linked list) :
Single linked-List (also called just linked-lists):
A linked list is dynamic data structure that let you store any type of data and with no size limits since it’s dynamic , but with a new concept so that each list element or also called node has :
- a value with a type specified at the declaration.
- a pointer that point to the address of the next node in the list.
- for the last node his next pointer points to the null value so it’s a special case that indicates that this is the end of the list.
How linked list are stored in memory ?
Not like the arrays that need to allocate a memory at the start of the creation because it has a known size that needed to be allocated , the linked list don’t need to allocate a contiguously space in the memory because each element has a pointer towards the next element of the list so it does not matter where is the place of the next element as long as it has it’s pointer it will always know where to go next until it reaches the null pointer (end of the linked list).
Where and Why we need linked-Lists ?
- implementing another data structures like stack queues and graphs.
- used to model real world problems like a trains.
- used as a solution for the hash collision problem in the hash data structures(a problem know in the hash based data structures) .
- one important this is that in arrays if you delete an element that element space still exists but you can do something like put a special character or number (based on the type) in it that it indicates that this element was deleted but the space will be always allocated and can’t be changed unless you delete the whole array but in the linked list as an advantage of the chaining concept with pointer you can delete an element and it’s space in the memory because the memory get allocated and freed each time you add or delete an element.
How can i implement a linked list ?
The code source for the Linked List implementation is in this file :
https://github.com/GourineAyoubPrf/ArrayAndLinkedLists/tree/main/src/arraysandlinkedlistes
this data structures are already implemented in most of the >languages . In our example we will use java language as a >tool to implement the linked list you can use any language >you want the concept want change just the syntax. Each >linked list has a pointer of the head and a size property >(you can add other properties if you want)and as we know >each node has a next pointer and a value.
Linked-lists operations complexity :
Add at head :
Since we already have the head pointer so this will take O(1) time complexity because we need just to change the pointer of the head to the new node and link the new node with the previous head.

Add at tail :
In this case we assumed that we don’t have a pointer of the tail so in order to get that we need to loop over all the list nodes then point the last node next pointer to the new node and point the next pointer of the new node to null so it indicates that it’s the last node.
you can make this also o(1) if you memorize the tail address >in your implementation.
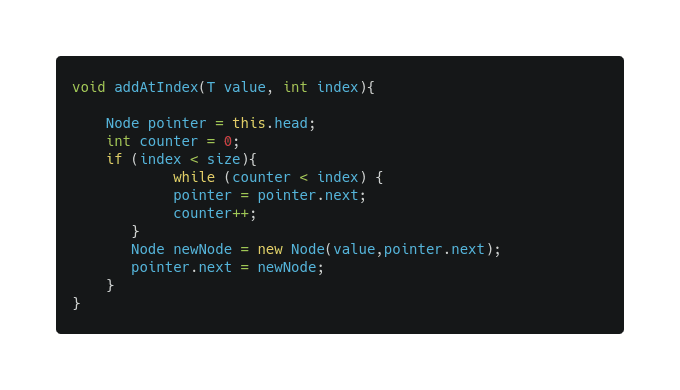
Add at a specified Index :
First we have to find the node that correspond to that index and for that we need to loop until we reach that node after that it’s just a matter of changing pointers the new node next pointer will point to the current node next and the current node next pointer will point to the new node and . And generally it will take O(n+1/2) time complexity so we can say it’s O(n).
Remove Head :
Since we have a head pointer this will be a O(1) time complexity and all what we need to do is :
- make the head pointer point to the current head next pointer then clear the head node.
in our case in java there is something called the garbage >collector so as long as an object has no reference to it it >will be cleared but in some other language you have to free >the space manually.
Remove tail :
Just as adding at the tail we need first to find the node that is before tile with a loop then we do the next :
- point the current node next to null. And this will take O(n) time complexity.

Remove at a specified index :
For this we have to loop over the list nodes so we can get the node that we are deleting after that we can do :
- point the next pointer of node that is before the index to the next of the deleted node.
and it will be an O(n) time complexity.

Search for a value:
It’s simple just a loop over using a pointer and if we reach the null pointer it means that the element was not found in the list , complexity will be O(n).

Double linked-lists :
A doubly linked list has the same behaviour as the normal linked list (single linked list) but each node has one more info and that is a pointer to the node that is before him so basically each node has 3 information :
- a pointer to node that is before him : before
- a value with a specific type : value.
- a pointer to the next node after him : next.
the head before pointer and the tail next pointer will be >null as indicator of the start and the end of the list.
How can i implement a double-linked-list ?
Each double linked list has a pointer at the head and the tail of the list and a size proprieties . Each node has tow pointer before and next and a value.
the implementation can be changed as you want as long as you >keep the same concept because at the end this data structure >is meant to help you not make it more complicated so you can >always tweak the implementation to solve the problem that >you want or add new operations for the list as you need.
Double-Linked-Lists operation complexity :
The code source for the Double linked lists implementation is in this file :
https://github.com/GourineAyoubPrf/ArrayAndLinkedLists/tree/main/src/arraysandlinkedlistes
Add at head :
The same it’s will stay o(1) and doing the flowing steps :
- point the new node “before” pointer to null.
- Point the “next” pointer of the new node to the head .
- Point the “before” pointer of the head to new node.
- Make the list head pointer points to the new node.

Add At tail :
This will be O(1) following the next steps , since we have a tail pointer we just need to do :
- point the head “next” pointer to the new node.
- point the new node “before” to the tail of the list.
- point the new node “next” pointer to null.
- make the tail of the list is the new node.

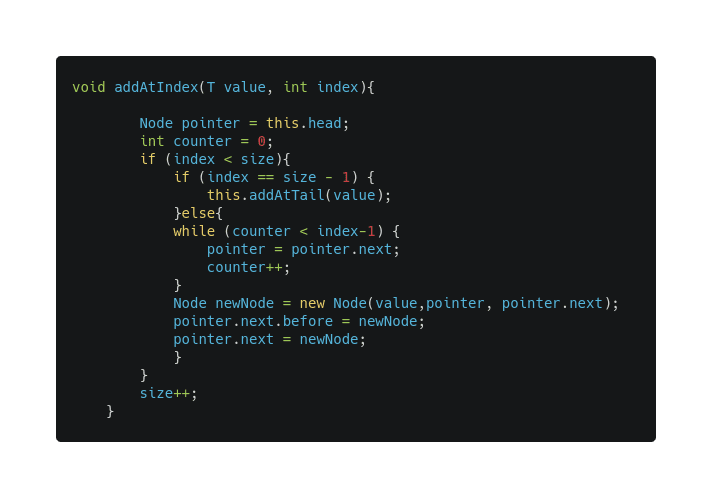
Add at a specified index :
Just as single linked list we need to loop over the list to fond the element with that node , the time complexity will be O(n) and the steps will be the following :
- find the node that correspond to that index (let’s name it node X).
- make the new node “before” pointer point to node X.
- make the new node “next” pointer points to node X “next” pointer.
- the previous “next” node of X (lets name it Y).
- make the “before” pointer of Y points to the new node.
- make node X “next” pointer points to the new node.
Remove at head :
Same as linked list will take O(1) :
- lets name the “next” node of the head node X.
- point node X “before’ pointer to null.
- the new head will be node X.
- garbage collector will do the rest since the head has no reference to it it’s space will be freed.

Remove at tail :
This will take O(1) time complexity with this steps :
- let’s name the node that is before the tails (the before of the tail) node X.
- point the node x “next” pointer to null.
- make the list tail point to the node x.

remove at a specified index :
This will be O(n) :
- first we need to find the node correspond to the index and we use 2 pointers.
- let’s name the node at the index node X.
- lets name the node before the node X node Y
- lets name the node that is after node X node Z.
- point node node Y “next” to node Z.
- point node Z “before” to the node Y.

the search operation is the same it will take O(n) time >complexity and the we use the same principal in searching >just a pointer that will loop until we reach the end.
Single linked list vs double linked list :
- single linked list will have no “before” pointer mean;s you can’t go backward but in the same time it will store less data.
- with double linked list you will have the ability to go through list in the tow direction but with the cost that it has more space cause it has 1 more information to store.
Circular linked List :
Circular linked list is another linked list type basically it;s the same as the double linked list but instead of the head before pointer point to null adn the tail next pointer point to null we have :
- the before pointer of the head will point to the list tail.
- the next pointer of the tail will point to the list head.
in this way the list will be circular in a way that you will loop over the list nodes as long as you want with no stop unless you store the head address or the tail address and check for them in order to stop.
Conclusion :
- arrays and linked list are tow of the most commune Data structures so any programmer or a software engineer need to know and understand how they work.
- when you want to choose what to use between arrays and linked list try to see what;s the most commune operation that will be done in your algorithm then base on that take the data structure that does that operation with less time complexity , as you know there is no good or bad data structure it;s all about what you are using in for.
- when you are using a programming language try to see the implementation and the method given to the data structure that you are using cause it may be different from one language to another.
- knowing the difference between how the linked list get stored in memory and how the dynamic arrays are stored in memory is so important not because they are both dynamic means that they have the same time complexity .
- hope you had a good reading and you benefited from the article , next article will be about tow other linear data structures : stacks and queues.
this article is also available in the medium website you can >visit this link :
https://gourineayoub-prf.medium.com/data-structures-and-complexity-part2-linear-data-part1-arrays-and-linked-lists-713a53360e64







Top comments (0)