Being a software engineer does not mean only that you should know how to build programmes it also means that you should aim for the best performance that you can get from what you are building to give the user the best experience , in order to do that as a software engineer you should know the different types of DS’s (data structures) and how to use theme plus how to get the best out of your solution using the complexity analysing.
Data structures :
Definition :
- My definition : data structure is a way of organizing data with some specific rules in order to solve various programming problems , each data structure has it’s own pros and cons or more like a place where it will be best to use it based on what it can offer to the programmer , each data structure has it’s own operations and relations between the data that it contains also the nature of the data that is stored in it.
- wiki : a data structure is a data organization, management, and storage format that enables efficient access and modification.More precisely, a data structure is a collection of data values, the relationships among them, and the functions or operations that can be applied to the data
- A data structure is a specialized format for organizing, processing, retrieving and storing data.
why we use data structures ?
- we use data structures as a tool for storing any kind of data that we are manipulating in our algorithm.
- Data structures are used in computing to make it easy to locate and retrieve information.
- without DS (Data structures) it will be impossible to treat a huge amount of data with no errors.
why you should learn data structures ?
- if you know a lot of DS it’s guaranteed that you will use the right DS in the right place.
- knowing more DS will make give you the ability to know how to lower the complexity (we will talk about it later ) and maximize the performance of your algorithms.
- a lot of famous algorithms is implemented in some specific DS so to understand it you have to understand the DS that is implemented with.
- you will have more than one solution for your problems so that you can choose the best one .
- save memory by using the best fit DS for your algorithms.
Data structures types :
there is a lot of DS each one has it’s own rules,way of manipulating,relations between it’s data , the format of it’s stored data , complexity but on general we can group the DSs in four forms :
- linear : list , arrays , stack ,queues, linked lists.
- trees : binary tree , AVL tree , black/red tree. , heaps …etc.
- hashes : hash-maps , hash-tables.
- graphs : decision, directed … etc
note : we will discuss each DS in depth in the next parts >of this articles series.
Types of operations that can we make for a data structure :
As a DS is way of organizing and manipulating data it means that we can apply some operation on the data that we are storing and basically the operation can be one of this following or ones that are similar to it :
- adding / pushing .
- removing / deleting .
- updating .
- sorting .
- merging .
- retrieving.
note :
- there is also other operation that can be done only to >some types of DS , so some operation are based on the type >of the DS that you are using each DS support a bunch of >operation.
- the way of the operation is handled and what is the >result of the operation may be different from one DS to >another based on how it store the data and manipulate it.
what is an algorithm complexity ?
in programming , solving the problem is not everything because some time the solution is not applicable in real world applications or it exceeds the resources that a company have so for the same problem most of the time there is more then one solution , the next step after finding a solution that works for the different test cases is to optimize it , and here we have tow axes that we focus on :
1. Time complexity :
it means the time that your algorithm will take to give a correct result after giving it an input (if there is inputs ) and to make it more formal when programmers study the complexity of there solution they use one of the complexity notation as an example big notation (will discuss later). we measure the time and complexity in terms of the growth and and the number of operations relative to the input size n.Usually, the time required by an algorithm falls under three types :
- Best Case − Minimum time required for program execution.
- Average Case − Average time required for program execution.
- Worst Case − Maximum time required for program execution.
2. space complexity :
Here we are talking about the amount of space your algorithm will allocate in order to solve the problem most of the time the space will be freed after the end of the algorithm(we are not talking about data base space here) but the problem is when your algorithm consumes a lot of memory by time your program will crush and it will cause the system to crush to.
note : in this article we focus more on time complexity.
Asymptotic bounds :
in order to measure the complexity we need some formal ways to do that for each solution and for that we have a 3 Asymptotic bounds :
- big-omega : which gives you the lower bound.
- big-o : which gives you the upper bound.
- big-theta : which gives you both the upper and lower bound.
note :
- The annotation it self is not related to the best,worst or >average solution , each annotation can be applied to >calculate worst, best or average of the solution that you >have done.
- big-Theta is good because it gives you both bounds but >it’s hard sometimes to prove it .
- if big-theta of a function f is X then it means that big-o >of this function f is also X but not the inverse unless that >big-omega is also equals to X.
- the Asymptotic bounds are based on a mathematical >functions and they allow you to give a complexity to a >solution that you implemented and by result you can compare >tow solutions and take the best based on that.
How to calculate Big-o notation ?
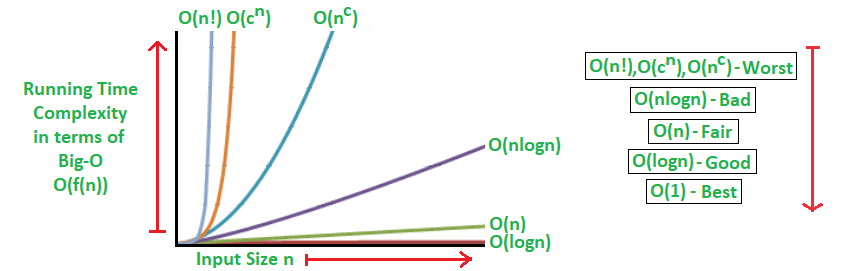
big-o is a notation used to the upper bound time of an algorithm it means the worst case scenario which we always get interested in because if the worst case is good for the you don’t have to worry about other cases.
note : some operation like push /pull / add has different >complexities based on the type of the data structure that >you are using as an example : to search for a value in a >hash-table DS that will be O(1) in best case and o(n) in >some other cases (hash collision cases) but in a linked-List >that will always be O(n).
asymptotic notations for the big-o :
1. constant O(1):
basically each simple instruction in your algorithm has a constant time complexity noted as O(1) this simple instruction are operations like this :
- a variable declaring.
- a value assigning to a variable.
- a condition test.
- accessing an array value by index.
2. logarithmic O(log n):
An algorithm is said to run in logarithmic time if its time execution is proportional to the logarithm of the input size. usually this type of complexity will exist if the number of iteration that you are doing in your program will get divided to half each iteration as an example : first iteration : 20 → second iteration : 10 → third iteration : 5 … etc.
This kind of behaviour is used in a one of the best algorithm paradigm know as divide and concur an as an example we have the binary search of a value in a sorted array :
in this algorithm the number of iteration is divided to half each time and we choose the half that we continue with based on the value of the searched element so the complexity here will be O(log n).
note : the data can be divided by more then 2 (in this case >the logarithm base get changed as example : divide by tow it >means log base 2 and if you divide by 4 it means log base 4 >…etc).
3. linear O(n) :
Linear time complexity will appear when we have to do a simple instruction but n times usually that n refers to the length of a data structures that we will loop overt it’s elements or a counter in a loop as an example a for loop with a condition of index< n where n is the length of our list :
so the complexity of this loop here is the complexity of the condition + the complexity of the loop core * n (number of repetitions) and since we take the worst case in big-o so we say that this complexity = O(1) + O(n) = O(n)
note : if the condition contains a function call or the loop >core itself contains a function call then we need to take >that in consideration and calculate the called function >complexity first then we multiply it by n(number of repetitions).
3. n log n complexity O(n log n) :
As we already talked about the O(log n) and the O(n) complexity the O(n log n) is just a form of repeating the log n complexity n times as an example we can take the quick sort algorithm as an example where the data will be divided and treat each half and sort it and repeat this until the table is sorted so we have the divide and concur mechanism that will take O(log n) time complexity and O(n) time complexity for the iteration through the table , in this implementation we are using a recursive mechanism :
the formula of complexity (because it;s recursive) is T(n) = 2T(n/2) + O(n) and after you solve it you will have a complexity of O(n log n).

4. quadratic O(n²):
this complexity appears often when we have a nested loop (a loop inside another loop) as in example the algorithm that prints all the elements of a matrix will be like this :
in this case we have the first loop that will repeat I times and inside it each time the second loop will repeat j times and since we consider the number of repeated times as n so we have n repeated n times so its O(n2)
note : In general, doing something with every item in one >dimension is linear, doing something with every item in two >dimensions is quadratic, and dividing the working area in >half is logarithmic.
5. cubic O(n³) :
Here we have the same principal as the quadratic complexity but we add one nested loop inside so it will be 3 loops as an example we have this situation : a list that has a matrix as a value and we need to loop every matrix and print it’s values.
since we already know that the complexity of the matrix print algorithm is O(n2) the we just have to multiply it by n and that give us O(n3).

6. exponential O(2^n) :
so we already know that in the logarithmic complexity the data is divided by tow but here we have the complexity will grow after each iteration , this is more likely to happen with recursive calls as an example the Fibonacci sequence algorithm :

7. factorial O(n!) :
this is one of the worst complexity that you should always avoid (if you can) and it appears in the problem of finding Find all permutations of a given set/string.
complexity for recursive functions :
for recursive function it’s a bit different to calculate the complexity since we have to do a mathematical analyses of the algorithm and proof it complexity throw the iterations , and there is also many rules depends on the shape of the recursive functions , example :
if we take the Fibonacci algorithm as an example and try to analyse it’s complexity we will find the next :
the if condition and the return 1 will always be of complexity O(n)
this line {return Fibonacci(n-1) + Fibonacci(n-2) } has tow functions calls it means in order to calculate it’s complexity we need to calculate the called functions complexity and since it the same function called in a recursively we need to format it in a formula :
Where T(n) = our complexity and n = the number that we want to calculate for the Fibonacci sequence. And c is a constant with O(1) complexity represent the first part before the functions call.
1et iteration : T(n) = T(n -1) + T(n-2) + c =
2end iteration : T(n) = 2 (T(n-1) + T(n-2) + c) + c
3ed iteration : T(n) = 2(2 (T(n-1) + T(n-2) + c) + c) + c
……
k iteration : 2^k * T(n — 2k) + (2^k — 1)*c // approximation.
After this you need to find the k value and replace it in the last formula to find the complexity. For this solution the complexity will be O(2^n)
note 1 : each recursive function will be solved in a >different way depends on the number of calls that it has and >the way of the data is handled (is the data getting smaller >by dividing or by subtracting a value from it …etc).
note 2 : sometimes to make the complexity better consider >using another approach for solving the same problem as an >example if you are using recursive way try using dynamic >programming (this paradigm will be discussed in the next >articles).
conclusion :
- Data structures is a major thing that you need to know at least the famous and most used of theme in order to become a better programmer , each time you learn a new DS you will have a new view or a new perspective on how to solve a problem based on the philosophy of that new DS and the more you get used to different DS the more different solution you can get for the same problem and the most important you will know which DS is the best to use with that problem ion order to give you the best performance.
- Time and Space complexity is a one of the important axis that based on we judge the efficiency and the quality of the solution and it goes along side with understanding the DS that you work with because if you don’t then you can’t neither calculate the complexity of your solution nor optimizing it .
- the more you solve programming problems and try to optimize them the more you will get experience and get to know a variant of new DSs , make sure you do your best and keep learning every day “ we are never old to learn new things “.
- hope you got some new information from this article and it benefited you , this article is just the first from a series of article that will discus different Data structures and it’s complexity.
this article is also posted on meduime : https://gourineayoub-prf.medium.com/data-structure-and-complexity-a-programmer-best-tow-weapons-part-1-introduction-a941cda2f557







Top comments (0)