GREEDY METHOD
•Greedy method is the most straightforward designed technique.
•As the name suggest they are short sighted in their approach taking decision on the basis of the information immediately at the hand without worrying about the effect these decision may have in the future.
DEFINITION:
•A problem with N inputs will have some constraints .any subsets that satisfy these constraints are called a feasible solution.
•A feasible solution that either maximize can minimize a given objectives function is called an optimal solution.
Control algorithm for Greedy Method:
1.Algorithm Greedy (a,n)
2.//a[1:n] contain the ‘n’ inputs
3. {
4.solution =0;//Initialise the solution.
5.For i=1 to n do
6.{
7.x=select(a);
8.if(feasible(solution,x))then
9.solution=union(solution,x);
10.}
11.return solution;
12.}
The function select an input from a[] and removes it. The select input value is assigned to X.
1.Feasible is a Boolean value function that determines whether X can be included into the solution vector.
2.The function Union combines X with The solution and updates the objective function.
3.The function Greedy describes the essential way that a greedy algorithm will once a particular problem is chosen ands the function subset, feasible & union are properly implemented.
KNAPSACK PROBLEM
•we are given n objects and knapsack or bag with capacity M object I has a weight Wi where I varies from 1 to N.
•The problem is we have to fill the bag with the help of N objects and the resulting profit has to be maximum.
•Formally the problem can be stated as
Maximize xipi subject to XiWi<=M Where Xi is the fraction of object and it lies between 0 to 1.
•There are so many ways to solve this problem, which will give many feasible solution for which we have to find the optimal solution.
•But in this algorithm, it will generate only one solution which is going to be feasible as well as optimal.
•First, we find the profit & weight rates of each and every object and sort it according to the descending order of the ratios.
•Select an object with highest p/w ratio and check whether its height is lesser than the capacity of the bag.
•If so place 1 unit of the first object and decrement .the capacity of the bag by the weight of the object you have placed.
•Repeat the above steps until the capacity of the bag becomes less than the weight of the object you have selected .in this case place a fraction of the object and come out of the loop.
•Whenever you selected.
ALGORITHM:
1.algorithm Greedyknapsack (m, n)
2.{
3.for i=1 to n do a[i]=0.0;
4.u=n;
5.for i=1 to n do
6.{
7.if (w[i]>u)then break;
8.x[i]=1.0;
9.u=u-w[i]
10.}
11.if(i<=n) then
12. x[i]=u/w[i];
13.}
Example: Capacity=20 n=3 ,m=20 Wi=18,15,10 Pi=25,24,15
Pi/Wi=25/18=1.36,24/15=1.6,15/10=1.5
Descending Order: Pi/Wi: 1.6 1.5 1.36
Pi = 24 15 25
Wi = 15 10 18
Xi = 1 5/10 0
PiXi=124+0.515: 31.5
The optimal solution is 31.5
JOB SCHEDULING WITH DEAD LINES
The problem is the number of jobs, their profit and deadlines will be given and we have to find a sequence of job, which will be completed within its deadlines, and it should yield a maximum profit.
Points To remember:
•To complete a job, one has to process the job or a action for one unit of time.
•Only one machine is available for processing jobs.
•A feasible solution for this problem is a subset of j of jobs such that each job in this subject can be completed by this deadline.
•If we select a job at that time.
Since one job can be processed in a single m/c. The other job has to be in its waiting state until the job is completed and the machine becomes free.
So the waiting time and the processing time should be less than or equal to the dead line of the job.
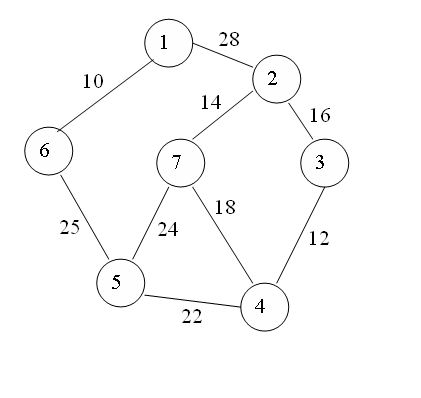
MINIMUM SPANNING TREE:
•Let G(V,E) be an undirected connected graph with vertices ‘v’ and edge ‘E’.
•A sub-graph t=(V,E’) of the G is a Spanning tree of G iff ‘t’ is a tree.3
•The problem is to generate a graph G’= (V,E) where ‘E’ is the subset of E,G’ is a Minimum spanning tree.
•Each and every edge will contain the given non-negative length .connect all the nodes with edge present in set E’ and weight has to be minimum.
NOTE:
We have to visit all the nodes.
The subset tree (i.e) any connected graph with ‘N’ vertices must have at least N-1 edges and also it does not form a cycle.
DEFINITION:
•A spanning tree of a graph is an undirected tree consisting of only those edge that are necessary to connect all the vertices in the original graph.
•A Spanning tree has a property that for any pair of vertices there exist only one path between them and the insertion of an edge to a spanning tree form a unique cycle.
Application of the spanning tree:
Analysis of electrical circuit.
Shortest route problems.
Minimum cost spanning tree:
•The cost of a spanning tree is the sum of cost of the edges in that trees.
•There are 2 method to determine a minimum cost spanning tree are
Kruskal’s Algorithm
Prom’s Algorithm.
KRUSKAL’S ALGORITHM:
In kruskal’s algorithm the selection function chooses edges in increasing order of length without worrying too much about their connection to previously chosen edges, except that never to form a cycle. The result is a forest of trees that grows until all the trees in a forest (all the components) merge in a single tree.
•In this algorithm, a minimum cost-spanning tree ‘T’ is built edge by edge.
•Edge are considered for inclusion in ‘T’ in increasing order of their cost.
•An edge is included in ‘T’ if it doesn’t form a cycle with edge already in T.
•To find the minimum cost spanning tree the edge are inserted to tree in increasing order of their cost.
Algorithm:
Algorithm kruskal(E,cost,n,t)
//Eàset of edges in G has ‘n’ vertices.
//cost[u,v]àcost of edge (u,v).tàset of edge in minimum cost spanning tree
// the first cost is returned.
{
for i=1 to n do parent[I]=-1;
I=0;mincost=0.0;
While((I<n-1)and (heap not empty)) do
{
j=find(n);
k=find(v);
if(j not equal k) than
{
i=i+1
t[i,1]=u;
t[i,2]=v;
mincost=mincost+cost[u,v];
union(j,k);
}
}
if(i notequal n-1) then write(“No spanning tree”)
else return minimum cost;
}
Analysis:
• The time complexity of minimum cost spanning tree algorithm in worst case is O(|E|log|E|), where E is the edge set of G.
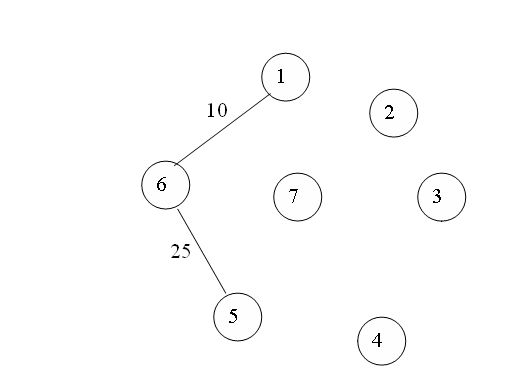
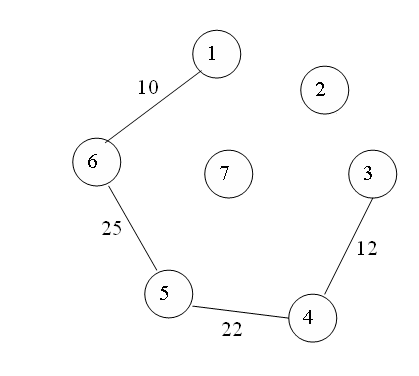
PRIM’S ALGORITHM:
Start from an arbitrary vertex (root). At each stage, add a new branch (edge) to the tree already constructed; the algorithm halts when all the vertices in the graph have been reached.
Algorithm prims(e,cost,n,t)
{
Let (k,l) be an edge of minimum cost in E;
Mincost :=cost[k,l];
T[1,1]:=k; t[1,2]:=l;
For I:=1 to n do
If (cost[i,l]<cost[i,k]) then near[i]:=l;
Else near[i]:=k;
Near[k]:=near[l]:=0;
For i:=2 to n-1 do
{
Let j be an index such that near[j]≠0 and
Cost[j,near[j]] is minimum;
T[i,1]:=j; t[i,2]:=near[j];
Mincost:=mincost+ Cost[j,near[j]];
Near[j]:=0;
For k:=0 to n do
If near((near[k]≠0) and (Cost[k,near[k]]>cost[k,j])) then
Near[k]:=j;
}
Return mincost;
}
•The prims algorithm will start with a tree that includes only a minimum cost edge of G.
•Then, edges are added to the tree one by one. the next edge (i,j) to be added in such that I is a vertex included in the tree, j is a vertex not yet included, and cost of (i,j), cost[i,j] is minimum among all the edges.
•The working of prims will be explained by following diagram.






Top comments (0)