This guide by Amit Patel was immensely helpful in building the math into my application and is widely regarded as the bible for hex-based games as far as I can tell from the dev community:
https://www.redblobgames.com/grids/hexagons/
Creating the Hex
This part is fairly straightforward: A hex has 6 corners equidistant from the center and has center coordinates with an x and y coordinate. The 6-pointy corners and the index of that corner are defined and the x and y of that corner is returned. Then there are functions built to draw line between the 6 corners.
Creating a Hex Grid with hexToPixel
Creating the hexagonal grid naturally required the single hexagon to be drawn repeatedly in a pattern of columns and rows in such a way that they formed an interlocking grid. Initially, I struggled to iterate the hexagons exactly together as there was always rounding that left pixels in between the hexagons. With much help on the math solution to this axial coordinates problem online, I finally worked out the offset system. The solution was to take the center of a single hex and offset to the next hex by a function that exactly calculated the distance to the next coordinate by pixels(in my case 32.234762 pixels between hexes). This allowed an iterative approach to exactly draw the hexes in the row and column formation of my chosen size.
pixelToHex
The opposite solution, to take a onMouseMove pixel location and map it to the coordinate system of the hex the mouse is currently on, required a bit more work. First the size of the hexes needed to be declared and then placed on the screen by defining the hex origin location(ie where I began drawing the hexes. Then the column(q), row(r), and side(s) of the hex location can be identified with the below math equations. From there, the float returned was rounded to the nearest hex coordinate location and the returned to the onMouseMove event for further actions.
DistanceLine Creation
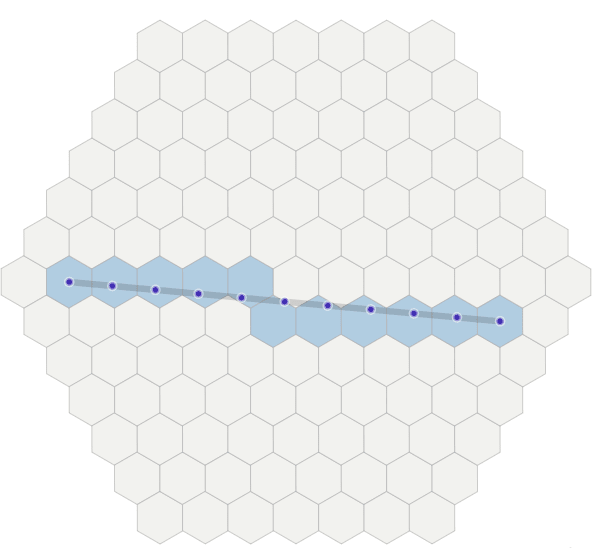
Another hard math problem: creating a hex to hex line form HexA to HexB. For this we need linear interpolation. Amit does a good job explaining this as follows for a sample distance of 10:
First we calculate N=10 to be the hex distance between the endpoints.
Then evenly sample N+1 points between point A and point B. Using linear interpolation, each point will be A + (B - A) * 1.0/N * i, for values of i from 0 to N, inclusive. In the diagram these sample points are the dark blue dots. This results in floating point coordinates.
Convert each sample point (float) back into a hex (int). The algorithm is called cube_round.
Converted to my game board where red it the player 1 position, blue is the player 2 position, lime is the mouse location, and orange is the distance path that I limit to 4:








Top comments (0)