Big O for the interview taker

Big O notation is a asympotic notation system used to define the scalability of algorithms. It measures how much a function grows referring to its computational or space endeavors.
Asympotic means that it refers to how much the function will change when it gets nearer and nearer to the desired result or infinity (if you wrote bad code).

Big O of one

There are many big O outputs, the most basic one is O(1), that stands for big O of one. It refers to an algorithm that doesn't matter the input, it will always take the same time or space to return the desired output.
An example may be a function that simply sums two numbers

public int sum(int a, int b) {
    return a + b;
}

Although there would be a difference between the sum of two numbers both less than ten and the one of two numbers higher than a million we are still using only one instructions with no extra variable that will always run only one time. It doesn't matter the input, the scalability of the algorithm will always be the same.
Another example of a O(1) algorithm would be the removal of the last node of a linked list. ```java public static boolean remove() { boolean flag = false; if (this.last != null) { if (this.last.next == null) { this.last = null; } else { this.last = this.last.next; } flag = true; } return flag; } ``` despite the input the algorithm, it will always take the same time to achieve the output.

Big O of N

O(n) happens when an algorithms scales directly based on the input. The most basic example of this big O case is the linear search into an array

public int linearSearch(int[] arr, int toSearch) {
    boolean found = false;
    int index = -1, i = 0;
    
    while (i < arr.length && !found) {
        if (arr[i] == toSearch) {
            found = true;
            index = i;
        }
    }
    
    return index;
}

Based on the length of the array (so of the size of the input) the algorithm is repeating its actions for n times.
It happens mostly in traversals and when we have are simply performing an action for every element of the input. Clearing a stack or a queue and just visiting an array, without any additional operation, would be O(n)

Big O of N squared

A situation of O(n²) happens when for every element of the input we perform an action on every single element of it, thus percorring the data structure n times itself.
Best examples of this are the basic sorting algorithms like bubble and insertion sorting

public static void bubbleSort(int[] arr) {
    boolean swapped = true;
    int i;
    
    while (swapped) {
        swapped = false;
        for (i = 0; i < arr.length - 1; ++i) {
            if (arr[i] > arr[i + 1]) {
                swapped = true;
                // computational swapping of elements
                arr[i] = arr[i] + arr[i + 1];
                arr[i + 1] = arr[i] - arr[i + 1];
                arr[i] = arr[i] - arr[i + 1];
            }
        }
    }
}

By reading a bit into the code you can quickly understand how bubble sort works. It goes throughout all of the array and if the next element is greater than the current it swaps them.
With an array like 3, 4, 2, 1 it would work like:

[0] [1] [2] [3]
 3   4   2   1
Is [0] greater than [1]? then swap them.
Is [1] greater than [2]? then swap them.
...
Is [2] greater than [3]? then swap them.

end of cycle

at the end of the first cycle we would have [4, 1, 2, 3] and we would go on till a single swap hasn't happened, which means that the array is finally fully sorted.
This is O(n²) because in the worst case the algorithm would traverse the array the size of itself times. If an array has size of four then 4 * 4 = 16, if 100 then 100 * 100 = 10000 times.
Sorting, be it an array or everything else, is a big deal in programming, especially in the production of large scale applications or services and a big O of n squared solution wouldn't be the most efficient. Usually, solutions with this big O are brutal force approches, also called naives. A solution like that for every problem is what first comes in mind to everyone when looking at a problem. If you think of a solution like this then there is problably a smarter way to solve the given problem.

big O of log N

In O(log n) the log stands for logarithmic. Glossing over the actual meaning of it and what is a logarithm, it simply means that at every iteration of the algorithmic the possibilities of reaching the desired result get halved at every single iteration. This is basically what happens in every divide & conquer algorithm, like binary search, and working with balanced trees.
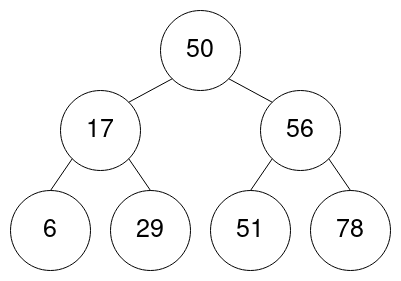
Having a balanced binary tree, something like:

how would we look for a specic number, let's say 29?
First of all we can define a single node as something like

public class TreeNode {
    int value;
    TreeNode left;
    TreeNode right;
    
    public TreeNode() {}
    // other various constructors
}

once we know what are working on we can build our lookup algorithm

public static boolean treeLookup(TreeNode root, int value) {
    boolean flag = false;
    Treenode temp = root;
    
    while ( temp != null && !flag) {
        if (temp.value == value) {
            flag = true;
        } else {
            if (value < temp.value) {
                temp = temp.left;
            } else {
                temp = temp.right;
            }
        }
    }
    
    return flag;
}

Why is treeLookup O(log n)?
We begin the loop while checking if the wanted value relies in the current root node. It being less than it we shift the current as its left child thus completely removing half of tree as possible location of the wanted node.
We do it again and go over the left side of the current node to focus on its right one and at the third iteraction we find the desidered node and confirm that it exists. At every iteration we halved the size of the input.

Big O of n log n

O(n log n) happens when while we are traversing our data structure we have to perform some sort of operations that involve halving it. With simpler word we are executing O(n) times an operation of O(log n). The most basic example of such big O is the merge sort.
This sorting algorithm consists of halving an array in till its minimum subarray and to perform the sorting while rebulding its subarrays. It is O(n log n) because the halving happens array.length times.

We aren't sorting the actual array but two subarrays every time and doing so is very easy, it is just the merging of two arrays but following the correct order.

Big O of potential n

Big O of potential is often presented as O(2^n) or O(m^n). This complexity is very rare and depicts the algorithms used to create all the possible combinations of something. It is often the complexity of backtracing algorithms. Let's take as an example the problem:

prompt: given a number n return in an array all its possible binary combination

first example:
    input: n = 2
    output: [00,01,10,11]

second example:
    input: n = 3
    output: [000,001,010,011,100,101,110,111]

This algorithm, by itself, is O(2^n). We have this complexity when we have to solve a recursive problem where we have to take every possible road and at every iteration we have two possible ways.
What if there are multiple ways to to walk at every iteration? This complexity refers to every time we have to compute every possible path and we can divide this kind of problems in two macro-groups: two possible ways and n ways. Although the algorithm would always be refereed as n factorial it is important to understand its differences. 90% of the times we'll have just two choices, we'll either pick or avoid the number, avoid or don't avoid that path and so on, but other times we don't know the possible path that may happen and so it becomes O(m^n). An example are all the possible different combinations of a matrix.