Expression Tree in Python

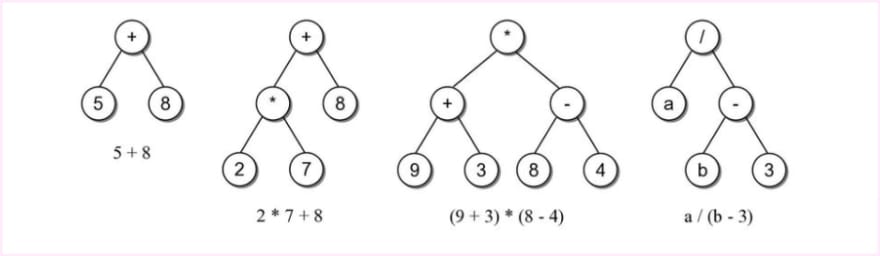
An Expression tree is a binary tree in which the operators are stored in the interior nodes and the operands are stored in the exterior nodes which are the leaves. An expression tree can be used to evaluate the expression or for converting an infix expression to either prefix or postfix notation.

Infix: An expression where the operator is placed in between the operands. \
Ex: (A+B) * (C-D) \
Prefix: An expression where the operator is in the expression before the operands. \
Ex: *+AB-CD

The expression tree structure is dependent on which the order of the operators is evaluated. The operator in every internal node is evaluated when each of its left and right subtrees is evaluated. In this manner, the lower an operator is in a subtree, the prior it will be evaluated. The root node contains the
operator to be evaluated.

Implementation:

To build expression trees, we use the stack data structure. We iterate over each character when a postfix string expression is passed and determine if it will be pushed on to our stack or not.

1. We push it onto the stack if the character is an operand. \
2. We pop two elements from the stack if the character is an operator, make them the character's left and right node child, and push the sequence back into the stack.

Note: Repeat the above steps until end of Prefix expression.

Ex:
Let’s pass the postfix expression “xy-” \
The first character is x; we push it onto the stack. The next character is y; we also push it onto the stack. The final character is the ‘-’ operator; we pop x and y and make them left and right child of ‘-’. So we end up with x - y as our Infix expression.

Program for Expression Tree:

# Python program for expression tree
# create a class for an expression tree node
class Expression_tree: 
    # Constructor to create a node
    def __init__(self , value):
        self.value = value
        self.left = None
        self.right = None
# function to check if 'c' is an operator
def isOperator(c):
    if (c == '+' or c == '-' or c == '*'
        or c == '/' or c == '^'):
        return True
    else:
        return False
# function to do inorder traversal
# Process all nodes of a tree by recursively processing the left subtree, the root, and finally the right subtree.
def inorder(t):
    if t is not None:
        inorder(t.left)
        print (t.value, end=" ")
        inorder(t.right)
# Returns root of constructed tree for given postfix expression
def constructTree(postfix):
    stack = []

    # Traverse through every character of input expression
    # Traverse - process every character in a string, from left end to right end. 
    for char in postfix :
       # if operand, push into stack
        if not isOperator(char):
            t = Expression_tree(char)
            stack.append(t)

        # Operator
        else:
            # Pop two top nodes
            t = Expression_tree(char)
            t1 = stack.pop()
            t2 = stack.pop()

            # make them left and right children
            t.right = t1
            t.left = t2

            # Add this subexpression to stack
            stack.append(t)

    # Only element  will be the root of expression tree
    t = stack.pop()

    return t
# Driver program to test above
postfix = "ab*ef-g+i-"
r = constructTree(postfix)
print ("Infix expression: ")
inorder(r)