The Sierpinski triangle is a famous mathematical figure which presents an interesting computer science problem: how to go about generating it. In this article I'll explain one method of generating the Sierpinski triangle recursively, with an implementation written in Vanilla JavaScript using HTML5 canvas. I'll also explain how to you'd go about downloading the contents of an HTML5 Canvas element as a PNG.
First, here's what the Sierpinski triangle looks like:
What is the Sierpinski Triangle?
The Sierpinski Triangle is a Fractal, Making it Naturally Recursive
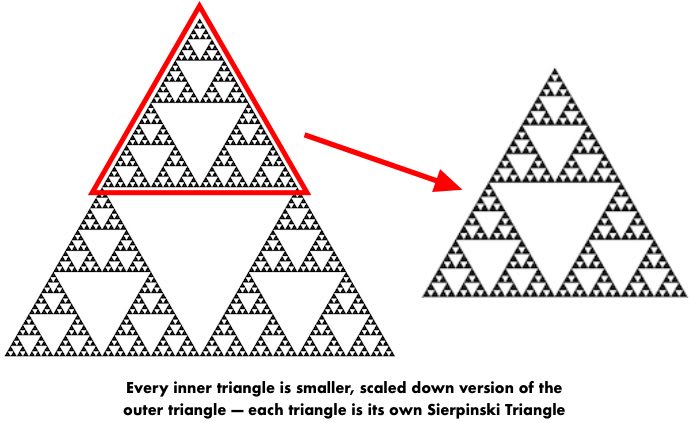
One initial thing to notice about the Sierpinski triangle is that every triangle is composed of smaller, identical triangles. Those triangles are also made up of even smaller, identical triangles, which are also made up of more triangles, and so on.
This property in which the Sierpinski triangle is made up of identical, scaled-down copies of itself makes it a fractal in mathematics. Fractals are shapes that are made up of scaled down copies of themselves. The Sierpinski triangle is actually arguably one of the most famous fractals that exist, along with Pythagoras Trees, the Mandelbrot set, and more.
The fact that fractals are made up of copies of themselves makes them naturally recursive, and it tends to be simpler to programmatically generate fractals recursively as supposed to using an iterative approach.
The Sierpinski Triangle Only Uses Equilateral Triangles
Next, notice how the Sierpinski triangle is made up of a single shape: the equilateral triangle. This is not a coincidence, and it is in fact one of the reasons the Sierpinski triangle is a notable mathematical figure.
The Sierpinski triangle takes advantage of a property of equilateral triangles: that they are one of the only shapes that can be made up solely by scaled down versions of itself, where a large equilateral triangle can be made by tesselating four equally smaller equilateral triangles. This makes them uniquely positioned to be the centerpiece of simple fractals, since it is intuitive to encompass smaller copies of an equilateral triangle inside a larger one.
This also makes it possible for fractals based on equilateral triangles, like the Sierpinski triangle, to be composed of only one shape. Other polygon-based fractals that don't use equilateral triangles often include several different shapes.
Generating the Sierpinski Triangle in JavaScript with HTML5 Canvas
Setting Up the HTML and Canvas Element
Let's start by setting up the canvas element and basic HTML markup:
<!DOCTYPE html>
<html>
<head>
<title>Sierpinski Triangle</title>
</head>
<body>
<canvas id="canvas" width="1000" height="1000"></canvas>
<!-- JavaScript Code Here -->
<script></script>
</body>
</html>
Note that the width and height variables in the canvas represent the inner dimensions of the canvas, not necessarily its size on the page. This means it can be resized in the future to fit different screen sizes, while maintaining its inner dimensions of 1000px by 1000px.
Creating Equilateral Triangles on the Canvas in JavaScript
Since equilateral triangles are the only shape used in the Sierpinski triangle, it makes sense to write a utility function to draw a given equilateral triangle on the canvas at a specified position and of a specified size.
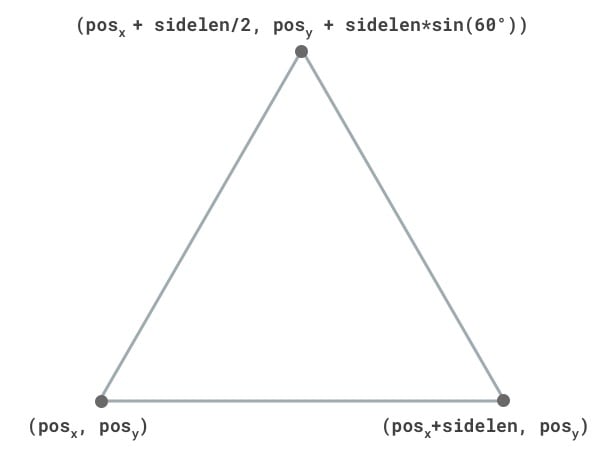
This function will take in two arguments: the position of the bottom left vertex on the triangle (pos), and the length of the sides of the triangle (sidelen).
To create polygons in HTML5 canvas, there are several functions to move to positions on the canvas, draw a path around an area of the canvas, and fill in that area. These include:
-
context.beginPath()andcontext.closePath()— create and close a path; commonly used withcontext.fill()after closing the path -
context.moveTo(x, y)— move to a position on the canvas. -
context.lineTo(x, y)— move to a position on the canvas while drawing a line from the current position. -
context.fill()— fill the most recent canvas path.
Creating a triangle simply means identifying the positions of the three vertices, drawing a path around those vertices, and filling the drawn area with a color. Identifying the positions of the vertices is pretty intuitive. Below is a visual showing the positions of the vertices. Note that the height of an equilateral triangle is mathematically equal to as sin(Pi/3) * sidelen.
With the positions of the vertices done, here's what the function to create an equilateral triangle on the canvas would look like:
const c = document.getElementById("canvas");
const ctx = c.getContext("2d"); // context variable is used to draw on a 2D plane
const createTriangle = (pos, sidelen) => {
ctx.beginPath();
ctx.moveTo(...pos); // go to the left vertex
// note that (0,0) in canvas is the top left, so 'up' on the vertical component would use substraction.
ctx.lineTo(pos[0] + sidelen / 2, pos[1] - sidelen * Math.sin(Math.PI/3)); // draw line from left vertex to top vertex
ctx.lineTo(pos[0] + sidelen, pos[1]); // draw line from top vertex to right vertex
ctx.lineTo(...pos); // draw line from right vertex back to left vertex
ctx.closePath();
ctx.fill(); // fill triangle
};
Implementing an Algorithm to Generate the Sierpinski Triangle
Now that the canvas and HTML has been set up and the createTriangle utility function has been written, we can start implementing an algorithm to generate the Sierpinski triangle.
Since fractals are naturally recursive, we'll use a recursive approach to generate the entire triangle.
First, recall that every triangle in the Sierpinski triangle is made up of three smaller triangles, one on the left, another on the right, and a final one on the top. Each smaller triangle is a copy of the outer triangle, the Sierpinski triangle. So, simply create a smaller Sierpinski triangle inside of each of the three triangles, and then more smaller Sierpinski triangles inside of those, and so on. Technically, the Sierpinski triangle repeats forever, but for visualizations like this, a stopping point should be defined when there have been enough repeats that the smallest triangles are hard to make out. At this point, filling in the smallest triangles acts as an effective substitution of repeating further.
To create this stopping condition, a variable called depth can be used. depth would represent the amount of times the program should continue repeating the fractal. depth should start at a certain value and decrease for every repeat, and every smaller Sierpinski triangle created. Once depth reaches zero (the base case), the program would stop and fill in the three triangles instead of continuing to repeat the fractal.
To create this functionality, let's create a function called createSierpinskiTriangle which takes the position of the Sierpinski triangle to generate, its side length, and the depth. The function should identify the positions of the three inner triangles, draw them if depth is equal to zero, or call createSierpinskiTriangle on the three inner triangles if the depth is greater than zero.
Here's what this would look like:
const createSierpinskiTriangle = (pos, sidelen, depth) => {
const innerTriangleSidelen = sidelen / 2; // side length of inner triangles is half the side length of the outer triangle
const innerTrianglesPositions = [
pos,
[ pos[0] + innerTriangleSidelen, pos[1] ],
[ pos[0] + innerTriangleSidelen / 2, pos[1] - Math.sin(Math.PI/3) * innerTriangleSidelen ]
]; // these positions are the same as what was used in the createTriangle function
if(depth === 0) {
innerTrianglesPositions.forEach((trianglePosition) => {
createTriangle(trianglePosition, innerTriangleSidelen);
});
} else {
innerTrianglesPositions.forEach((trianglePosition) => {
createSierpinskiTriangle(trianglePosition, innerTriangleSidelen, depth - 1);
});
}
}
To call the function, draw the Sierpinski triangle at the bottom left of the canvas ((0, 1000)) with a side length of 1000px (the width of the canvas) and a depth of 5.
createSierpinskiTriangle([0, 1000], 1000, 5);
Here's the result:
Try increasing the depth, and you should see that the triangle gets more and more detailed. Increasing the depth by one will result in three times the amount of total triangles to be drawn, so very high depths like 20 might not be performant since the canvas would have to draw 3^20 (~3.5 billion) triangles.
Downloading the Generated Triangle From the Canvas as a PNG
Now that we've generated the triangle recursively, one thing you may want to do is download the generated Sierpinski triangle as an image on your computer. Luckily, this is very simple to do in HTML5 Canvas.
First, the canvas must be converted to a data URL. If you're not familiar with data URLs, here's a simple definition:
A data URL is a URL scheme that allows data and files (images, audio files, etc.) to be respresented in a single URL containing all of the data. For example, if one wanted to include an image on a website, you would add the image to the web server and link to it in the HTML. With data URLs, the data URL contains the contents of the entire file, so it can simply be put into the HTML directly. This is useful in canvas because we want to export the image without it having a specific public URL, and data URLs allow that to be done.
The contents of the canvas element can be converted to a data URL with the .toDataURL method.
Next, let's download the data URL into the user's machine. In HTML, downloading a file is done by clicking a link and specifying the download attribute. For example, here's how someone would download an image as myimage.png when the user clicks a link: <a href="image.png" download="myimage.png">download!</a>.
Downloading a file through JavaScript is as simple as creating a link element with the specified href and download attributes, and artificially clicking on it.
Here's what this would look like:
const downloadCanvasContents = () => {
const link = document.createElement('a'); // create link element
link.download = 'Sierpinski Triangle.png'; // set download attribute
link.href = c.toDataURL(); // set the link's URL to the data URL to be downloaded
link.click(); // click the element and download on the user's browser
}
Try running downloadCanvasContents() in the JavaScript console after the Sierpinski triangle has been generated! An image should be downloaded to your machine with the contents of the canvas element.
To create a download button, adding a simple HTML button with the onclick attribute set to the downloadCanvasContents function should suffice.
<button onclick="downloadCanvasContents()">Download Generated Sierpinski Triangle</button>
Final Code and Conclusion
I hope you enjoyed this article, and found it interesting in generating the Sierpinski triangle with HTML5 canvas. For more mathematical background on the Sierpinski triangle and its history, I would recommend taking a look at the Sierpinski Triangle Page on Wolfram MathWorld and the Sierpinski Triangle Wikipedia Page.
Feel free to take a look at the final code.
Thanks for scrolling.
— Gabriel Romualdo, November 20, 2020








Top comments (4)
Congratulations and thanks!!
Love it!
Amazing!
good