<< #20 Breadth-First Search | View Solution on GitHub | #22 Sum of Three+ >>

(Image: FollowingNature on Flickr)
In the previous article, we discussed the differences between breadth- and depth-first search for trees and graph problems. Today, we're going to actually look at a sample problem, and given our new toolbox of search strategies, figure out the best way to implement a solution.
Here's the problem from LeetCode.
# Given the root of a binary tree, check whether it is
# a mirror of itself (i.e., symmetric around its center).
Let's look at some examples.
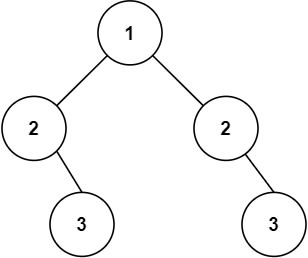
Giving the function the root of the above tree would yield True, since the values in the left half of the tree mirror the values in the right.
In the above tree, the nodes with 3 are not organized to mirror each other. Passing the root would yield False.
1. Strategy
As with binary tree problems, the first thing we want to ask is if we should use breadth- or depth-first search. At first glance, you might think BFS would make sense, seeing that all the nodes are the same across the first two levels. But once we look at the third level with the nodes 3, 4, 4, 3, suddenly, it gets more complicated. Instead, what if we split the tree into two halves and ran a depth-first-search on each half? Let's look at the first example again:
If we were to look at the left half, depth-first-traversal would read the nodes in the order: 2, 3, 4. At the same time, we can travel down the right side of the tree and print the same 2, 3, 4. We then conclude the tree is symmetrical.
2. Setup
The first thing we'll need is our TreeNode class. As always, it will take data, the value we want to store on the node, and then a left and right pointer, which are initialized to None.
class TreeNode:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
Next, we define our method, which takes in one value: the root node of the tree.
def is_mirror(root):
pass
Remember how we said we would split the tree into two halves, and then check the nodes in each half? We'll do that by calling a recursive helper method, check_halves. This method takes a left and right node, which will be root.left and root.right to start.
def is_mirror(root):
return check_halves(root.left, root.right)
3. Traversal
As with most tree traversals, we'll be using recursion. Start by defining our helper method that takes in a left and right tree.
def check_halves(left, right):
What is our base case? The simplest example would be a tree with only the root node, whose left and right halves are both None. In this case, we return True.
def check_halves(left, right):
if not left and not right:
return True
What's next? We want to check that there are both a left and right node, and that their values match. These can be put in the same if statement, but I'll separate them for clarity.
def check_halves(left, right):
if not left and not right:
return True
if left and right:
if left.data == right.data:
Next, we recurse! Here, we'll do a depth-first traversal on the left and right halves of the tree.
left_half = check_halves(left.left, right.right)
right_half = check_halves(left.right, right.left)
Then, we check to see if they are both True. This can be achieved with an and statement.
return left_half and right_half
Finally, we return the False if the previous if condition was not met. Altogether, our helper method looks like this:
def check_halves(left, right):
if not left and not right:
return True
if left and right:
if left.data == right.data:
left_half = check_halves(left.left, right.right)
right_half = check_halves(left.right, right.left)
return left_half and right_half
return False
4. Test it Out
The following code will build the tree from the example.
tree1 = TreeNode(1)
tree1.left = TreeNode(2)
tree1.right = TreeNode(2)
tree1.left.left = TreeNode(3)
tree1.right.right = TreeNode(3)
tree1.left.right = TreeNode(4)
tree1.right.left = TreeNode(4)
Now we just have to call print(is_mirror(tree1)) and it will print True. Success!
Let's try a tree that isn't symmetrical, like the second example. The two nodes with the value 3 aren't positioned to mirror each other.
tree2 = TreeNode(1)
tree2.left = TreeNode(2)
tree2.right = TreeNode(2)
tree2.left.left = TreeNode(3)
tree2.right.left = TreeNode(3)
Printing is_mirror(tree2) should give us False. The same will work if we change any values in the first tree so that they don't match left and right.
That's it for this week, I hope this was a good lesson on how to use DFS concepts to solve a Binary Tree problem. In a future article, we'll take a look at a problem where a breadth first approach would work better.
<< #20 Breadth-First Search | View Solution on GitHub | #22 Sum of Three+ >>
Sheamus Heikkila is formerly a Teaching Assistant at General Assembly. This blog is not associated with GA.








Top comments (0)