More Python Binary Trees: What is Breadth vs Depth First Search?

<< #19: JS Arrays | View Solution on GitHub | #21: Mirror Tree >>

IRL Breadth and Depth. (Images: 48days.com, deeperblue.com)

Christmas is over, but the classic data structure Binary Trees is forever. At least, technical hiring managers seem to think so. And when you're asked to solve a binary tree problem on an interview, the first thing your interviewer will want to know is this: breadth or depth first?

What's the difference?

Breadth First Search and Depth First Search, or BFS and DFS, are exactly as they sound--it's about the order of nodes we visit when traversing a tree. Depth first travels down the tree before traveling across, and breadth is just the opposite--start with the root and work down to its children, and then its children's children, and so on.

(Image: GeeksForGeeks)

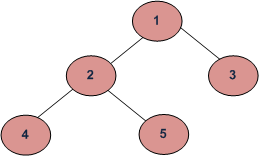
For example, in the above tree, a BFS approach would yield 1, 2, 3, 4, 5.

For DFS, there are multiple possible outcomes depending on if we do a Pre-, Post-, or In- order traversal. For example, Pre-order would yield 1, 2, 4, 5, 3. We've covered these three traversals in this article.

Implementing Breadth First Search in Python

Let's look at how we would do a BFS in Python. Start by defining our TreeNode class, which simply needs a value, and a left and right pointer.

class TreeNode:
  def __init__(self, value):
    self.value = value
    self.left = None
    self.right = None

1. Strategy

Here's how we will approach traversing each node by level:

1. Find the full height of the tree from root to farthest leaf.
2. Loop over each level (ending with the height)
3. Traverse to each level and print all the nodes on that level.

2. Find the Height of the Tree

In order to traverse over each level, we need to know how many levels there are in the tree. We'll write a method to traverse the tree and find its height.

def height(node):

You guessed it--this is going to be a recursive method, as are most binary tree traversals. Let's think of our base case. The simplest case is if we're given a null root, in which case the height is 0. You might say a node with no children is the simplest case, but then we have to check for its children, which adds to the complexity.

def height(node):
  if not node:
    return 0

What next? We have the left and right halves of the tree to traverse. So we'll call the height() method on those halves and save them to two variables, l_height and r_height.

def height(node):
  if not node:
    return 0
  l_height = height(node.left) 
  r_height = height(node.right) 

Which height do we return, left or right? Why, the higher one, of course! So we'll take the max() of both values, and return that. Don't forget to add 1 for the current node.

def height(node):
  if not node:
    return 0
  l_height = height(node.left) 
  r_height = height(node.right) 

  return max(l_height, r_height) + 1

3. Loop Over Each Level

Now that we have our height, we're ready to begin writing our breadth first traversal method. The only argument it takes is the root node.

def breadth_first(root):

Next, we get our height.

def breadth_first(root):
  h = height(root)

Finally, we loop over the height of the tree. For each height, we're going to call a helper function, print_level() which takes the root node and the level.

def breadth_first(root):
  h = height(root)
  for i in range(h):
    print_level(root, i)

4. Traverse the Tree

For each level, we're going to traverse down to the nodes at that level and print them. This will be achieved through our helper function. It takes in two arguments, the root node and the current level.

def print_level(root, level):

For this method, the level initially refers to the index i from the for loop. To traverse to the tree, we're going to recursively go down each level, subtracting from i each time until we hit level 0. This means we're at our level of interest, and we can print the nodes.

Again, our base case is if the root is null. This method only prints the tree, and doesn't return anything, so we'll simply return.

def print_level(root, level):
  if not root:
    return

Next, if our level is 0, i.e. the level we're interested in, we want to print the value at that node.

def print_level(root, level):
  if not root:
    return
  if level == 0:
    print(root.value)

Finally, if our level is greater than zero, that means we have to traverse down the tree. We call our recursive method on the left and right halves of the tree. Remember to subtract 1 from level in both function calls.

def print_level(root, level):
  if not root:
    return
  if level == 0:
    print(root.value)
  elif level > 0:
    print_level(root.left, level - 1)
    print_level(root.right, level - 1)

And that's it! It took three separate methods, but we're finally able to do a breadth-first traversal of the tree.

5. Test it Out

First, make a tree using our TreeNode class.

tree = TreeNode(1)

(Image: GeeksForGeeks)

Next, populate the rest of the tree. The following is to populate for the tree in the above image.

tree.left = TreeNode(2)
tree.right = TreeNode(3)
tree.left.left = TreeNode(4)
tree.left.right = TreeNode(5) 

Finally, we run our method.

breadth_first(tree)

This should print out 1, 2, 3, 4, 5. We've successfully traversed the tree!

If you have any ideas for problems or data structures you want to see covered on here, let me know in the comments! Thanks for reading.

<< #19: JS Arrays | View Solution on GitHub | #21: Mirror Tree >>

Sheamus Heikkila is formerly a Teaching Assistant at General Assembly. This blog is not associated with GA.

Comments

[mleecollege]

One con of this approach is that we have to traverse the tree from the root to print each level.