At an atomic level, Machine Learning is about predicting the future based on the past. For instance, you may wish to predict which team will win the upcoming Cricket World Cup. You will need to consider various factors for doing the prediction, like: type of pitch, weather conditions, number of spin bowlers, strike rate, the record of the team in the last five matches, etc. In a nutshell, a model will make predictions on unseen data by learning from the past data.
Now, what does learning actually means? What does it mean when we say that the model should learn well?
Let’s take this example:
John is taking a course on Linear Algebra, and at the end of the course, he is expected to take a exam to understand if he has “learned” the topic properly or not. If he scores well in the exam, it means that he has learned well. And if he fails, he hasn’t learned the topic properly.
But what makes a reasonable exam? If the questions in a linear algebra exam are based on Chemistry, then the exam won’t tell how well John has learned linear algebra, and if every question in the exam comes from the examples which John went through during his linear algebra classes, then it’s a bad test of John’s learning. Thus, in order to make a reasonable test, the questions should be new but related to the examples covered in the course. This tests if John has the ability to generalize. Generalization is perhaps a very important part of Machine Learning.
Let’s take the example of a course recommendation system for computer science students. It will predict how much a specific student will like a particular course. A student has been given a subset of courses and has evaluated the previously taken courses from them by giving them a rating from -2 (worst) to +2 (excellent). The job of the recommender system is to predict how much a particular student (say, John) will like a particular course (say, Deep Learning).
Now we can be unfair to this system: let’s say we ask the system to predict how much John will like a course on Energy Sciences. This is unfair because the system has no idea what Energy Sciences even is, and has no prior experience with this course. On the other hand, we could ask how much John liked the Natural Language Processing course which he took last year and rated +2 (excellent for it). In this case, the system will tell us that John will like this course, but it’s not the real test of the model’s learning since it’s just recalling it’s past experience. In the former case, we are expecting the system to generalize beyond its experiences, which is unfair. In the latter case, we are not expecting it to generalize at all.
The objects that our model will be making predictions about are called examples. In the recommender system, the example would be a Student/Course pair and the prediction would be the rating. We are given training data on which our algorithm is expected to learn. This training data is the historical rating data for the recommender system which it will use to make predictions for the test data. The system will create an inductive function f from this training data that will map the new example to the corresponding prediction. The function will take two parameters (Student, Course).
Function f (John/Machine Learning) would predict that John will like Machine Learning since the model knows that he took Natural Language Processing course in the past, which he liked. This is the art of inducing intelligence in the model. Thus, the system shows generalization. The data on which the system will make predictions is called as a test set. The test set should always be a secret. If the model gets to peek at it ahead of the time, it’s going to cheat and do better than it should.
The Decision Tree Model of Learning
The Decision Tree is a very classic model of learning which works on the “divide and conquer” strategy. Decision Trees can be applied to various learning problems like regression, binary and multiclass classification, Ranking, etc. We would consider binary classification in our case.
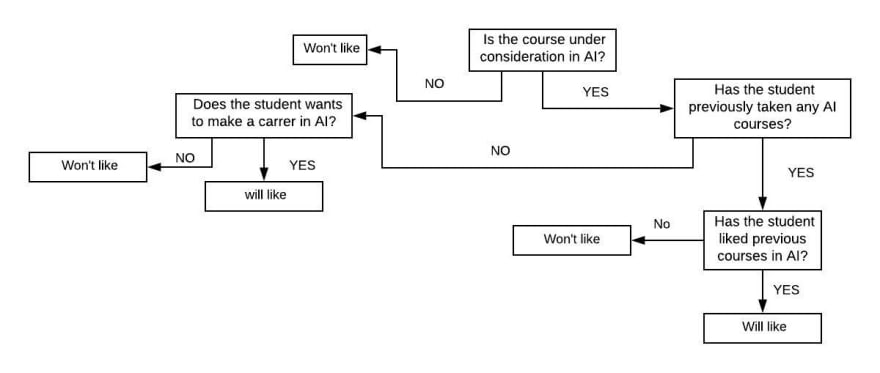
Suppose your goal is to predict if some unknown student will enjoy some unknown course. The output should be simply “yes” or “no”. You are allowed to ask as many binary questions as you can to get the output.
Consider this example:
You: Is the course under consideration in AI?
Ans: Yes
You: Has the student previously taken any AI courses?
Ans: Yes
You: Has the student liked previous courses in AI?
Ans: Yes
You: Does the student wants to make a career in AI?
Ans: Yes
You: I predict this student will like AI course.
Based on these binary questions, we will generate a decision tree.
How to check how well a model has performed?
To check how accurate the model’s performance is, we make a function for it, which we usually refer to as a loss function l(y, y’). Different learning problems have different forms of loss function. For regression, it’s a squared loss function (y-y’)^2 and for binary/multiclass classification, it’s zero/one loss function.
zero/one loss: l(y, y’) = { 0, y=y’ }
{ 1, otherwise }
Where y is the actual value and y’ is the predicted value.
The lesser the error while predicting, the more generalized is the model.
Why do we have different loss functions for different learning problems? And why do we have different learning problems in the first place?
Here are some of the learning problems:
Regression: predicting discrete future values based on past data. Example: The amount of rainfall on next Sunday.
Binary Classification: non-discrete binary values. Example: would it rain on Sunday or not? It will give 0 for No and 1 for yes.
Multiclass Classification: putting an example into one of a number of classes. Example: if a particular course belongs to computer science or earth sciences or educational sciences.
Ranking: putting the objects in a set of relevance. Example: arranging search results based on the user’s query.
The main reason to break learning problems into different genres is for measuring the error. A good model is the one that makes “good predictions”. Now, what do good predictions mean? Different types of learning problems differ in the way they define goodness. For example: predicting a rainfall that is off by 0.5 cm is much better than off by 300 cm. The same does not hold for multiclass classification. There, predicting computer science instead of earth sciences would be horrifying. Here, we can’t even afford slightest of the error. This is the reason why we break the problems into different categories and hence they have different loss functions. Thus, a good model is one that can generalize itself and can perform well on the unseen data.
Please, feel free to provide me any feedback and corrections on this piece. In the next article, I’m planning to talk about implementing a decision tree classifier and introducing inductive bias in the learning. You can also check out my previous article on Natural Language Processing over here


Top comments (0)