I. Test task
This test is to calculate the distance between two objects based on their positions and then decide whether to establish an association relationship. This is a typical non-equivalence association operation, which cannot be optimized with HASH algorithm.
This test originates from the celestial objects (“objects” for short) clustering operation of NAOC, and is conducted based on the simplified operation described below:
There are n objects in a photo of objects, and each object has various properties. One object and its properties form a record, and all objects and their properties in a photo form one table.
Now we have the data of two photos, which are stored respectively in tables A and B. The structures of the two tables are the same:
| Column name | Data type | Notes |
|---|---|---|
| SN | int | The serial number of an object, starting from 0 |
| InputMAGG | decimal | The properties of an object. In the end, we need to aggregate the properties of all records determined as the same object and calculate the average |
| OnOrbitRA | decimal | Right ascension in the position coordinate of an object |
| OnOrbitDec | decimal | Declination in the position coordinate of an object |
Structure of the generated result table:
| Column name | Data type | Notes |
|---|---|---|
| SN | int | For the matching object, the SN is the one in the first table; for the unmatching object, the SN is its own SN |
| CNT | int | The number of the matching objects; fill in 1 for unmatching objects |
| SN_COM | varchar | The SN of the matching objects, concatenate them as a string using underscore; fill in null for the unmatching objects |
| InputMAGG | decimal | The average of InputMAGG of the matching objects; fill in their own InputMAGG for the unmatching objects |
| OnOrbitRA | decimal | The average of OnOrbitRA of the matching objects; fill in their own OnOrbitRA for the unmatching objects |
| OnOrbitDec | decimal | The average of OnOrbitDec of the matching objects; fill in their own OnOrbitDec for the unmatching objects |
Calculate the distance between an object in photo A and an object in photo B. If the distance is less than a certain threshold, the two objects are considered to be the same object, and then generate a result table according to the above requirements.
SN is the serial number of an object. The SNs in both tables A and B are sorted in an ascending order, and each SN is unique. For a certain record in table A, traverse from the first record of table B, and stop traversing once a record is determined as the same object (the distance is smaller than a threshold), which means that among table B’s all records that satisfy the distance condition of the same record in table A, only the record with the minimum SN value is considered as being the same object as the corresponding record in Table.
Having determined that a certain record in table B and a certain record in table A are the same object, the said record in table B will no longer be calculated when calculating the next object in table A. In other words, the record in table B can only be matched once at most.
For the unmatching records in tables A and B, merge them into the result table. The null value in the SN_COM field means there is no matching object, and the value 1 in the CNT field indicates there is only one matching object.
Distance between objects
The position coordinate of an object on the celestial sphere is represented by (ra, dec), where ra is the right ascension and dec is the declination (equivalent to the longitude and latitude of the earth).
If the position coordinate of object1 on the celestial sphere is (ra1,dec1), and that of object2 is (ra2,dec2), the distance (dis) between them is calculated as follows:
The matching criterion of two objects is the calculation result of dis<=D, where D is a specified parameter, which is set as 0.3/3600 in this test.
The dec and ra in this formula correspond to OnOrbitDec and OnOrbitRa in the table structure respectively.
delta for preliminary screening
The above calculation formula is relatively complex and involves a large amount of computation.
We can prove the following conclusion mathematically. If the above formular is satisfied, there must be the following inequality:
And there exists a delta such that:
Therefore, we can utilize this simple condition to do a preliminary screening. If this condition is not met, then the complex condition above will definitely not be met.
The method to calculate delta:
![]() , it is the maximum absolute value of all decs in the data.
, it is the maximum absolute value of all decs in the data.
If one ![]() , then
, then ![]() ; if two
; if two ![]() , choosing one will be OK.
, choosing one will be OK.
If two
![]() , then
, then
![]() .
.
II. Technologies to be compared
We select two kinds of databases to make a comparison:
Starrocks, which is claimed to be the fastest SQL-based data warehouse. Starrocks 3.0 is to be tested.
Oracle, which is widely used, and often serves as a benchmark in database performance test. Oracle 19 is to be tested.
Currently, SPL does not provide vector-based calculation for trigonometric function, so SPL Enterprise Edition does not have a significant advantage. In this test, only SPL Community Edition (version 20230528) is tested.
III. Test environment and data
One physical server with the following configuration:
2 x Intel3014 CPUs, main frequency 1.7G, 12 cores in total
64G memory
SSD (Solid State Drive)
Virtual machine configuration:
Operating system: Red Hat 4.8.5-44
VM1: 8 CPUs, 32G memory
VM2: 4 CPUs, 16G memory
Since most of the applications will run on virtual machine at present, we conduct the test directly on virtual machine to examine the performance of the TUT (technology under test) on virtual machine and the sensitivity of TUT to the number of CPU cores and the capacity of memory. Based on the relatively common cloud VM specifications in the industry, we design two test environments VM1 and VM2 mentioned above.
For Starrocks, at least two nodes, BE and FE, need to be installed. The BE that undertakes computing task is installed on the VM, and the FE that undertakes management task is installed on the physical machine to avoid affecting the test results. For SPL and Oracle, they only need to be installed on VM.
This test provides three data scales for table A and table B respectively, that is, 10,000 rows, 100,000 rows and 500,000 rows. The following is the data compression package for download:
IV. Test SQL (Starrocks)
Description of SQL’s coding logic:
Convert OnOrbitRA and OnOrbitDec in tables A and B from angle to radian, and calculate their sin and cos values in advance.
Associate table A with table B (association criteria: dis<=D), and perform a preliminary screening, i.e., |dec1-dec2|<=D and |ra1-ra2|<=delta.
The “1.6548341646645552E-6” in the SQL code below is the delta calculated in advance.
Group the records by the SN of table A; sort each group’s records by the SN of table B; calculate out the serial number of records; filter out the records whose serial number is 1, which are the matching object.
Calculate the average of OnOrbitRA, OnOrbitDec and InputMAGG of the matching objects respectively according to requirements; concatenate the SNs with “_” to serve as the value of SN_COM field; store the number of the matching objects to the CNT field.
For the unmatching records in tables A and B, fill in null in SN_COM field, fill in 1 in CNT field, and merge them into the result set.
WITH A AS(
SELECT SN,
OnOrbitRA,
OnOrbitDec,
InputMAGG,
PI()/180*OnOrbitRA RA,
PI()/180*OnOrbitDec aDEC,
SIN(PI()/180*OnOrbitDec) SIN_DEC,
COS(PI()/180*OnOrbitDec) COS_DEC
FROM A
),
B AS(
SELECT SN,
OnOrbitRA,
OnOrbitDec,
InputMAGG,
PI()/180*OnOrbitRA RA,
PI()/180*OnOrbitDec aDEC,
SIN(PI()/180*OnOrbitDec) SIN_DEC,
COS(PI()/180*OnOrbitDec) COS_DEC
FROM B
),
T0 AS (
SELECT A.SN A_SN,B.SN B_SN,
B.OnOrbitRA B_OnOrbitRA,B.OnOrbitDec B_OnOrbitDec,B.InputMAGG B_InputMAGG,
A.OnOrbitRA A_OnOrbitRA,A.OnOrbitDec A_OnOrbitDec,A.InputMAGG A_InputMAGG
FROM A JOIN B
ON A.OnOrbitDec>=B.OnOrbitDec-0.5/3600
and A.OnOrbitDec<=B.OnOrbitDec+0.5/3600
and A.RA>=B.RA-1.6548341646645552E-6
and A.RA<=B.RA+1.6548341646645552E-6
and (SQRT(POWER(B.COS_DEC*SIN(A.RA-B.RA),2)
+POWER(A.COS_DEC*B.SIN_DEC-A.SIN_DEC*B.COS_DEC*COS(A.RA-B.RA),2))
/(A.SIN_DEC*B.SIN_DEC+A.COS_DEC*B.COS_DEC*COS(A.RA-B.RA)))
<=TAN((PI()/180)*(0.3/3600))
),
T1 AS (
SELECT *,ROW_NUMBER() OVER ( PARTITION BY B_SN ORDER BY A_SN ) RN
FROM T0
),
T2 AS (
SELECT * FROM T1 WHERE RN=1
),
T3 AS (
SELECT A_SN SN,
1+COUNT(*) CNT,
CONCAT(CAST(A_SN AS VARCHAR(1000)), '_', GROUP_CONCAT(CAST(B_SN AS VARCHAR(1000)),'_')) SN_COM,
(A_OnOrbitRA+SUM(B_OnOrbitRA))/(COUNT(*)+1) OnOrbitRA,
(A_OnOrbitDec+SUM(B_OnOrbitDec))/(COUNT(*)+1) OnOrbitDec,
(A_InputMAGG+SUM(B_InputMAGG))/(COUNT(*)+1) InputMAGG
FROM T2
GROUP BY A_SN,A_OnOrbitRA,A_OnOrbitDec,A_InputMAGG
)
SELECT * FROM T3
UNION ALL
SELECT SN, 1 CNT, NULL SN_COM, OnOrbitRA, OnOrbitDec, InputMAGG
FROM A
WHERE NOT SN IN ( SELECT A_SN FROM T1 )
UNION ALL
SELECT SN, 1 CNT, NULL SN_COM, OnOrbitRA, OnOrbitDec, InputMAGG
FROM B
WHERE NOT SN IN ( SELECT B_SN FROM T1 );
V. Test SQL (Oracle)
The SQL coding logic of Oracle is the same as that of Starrocks, except for differences in syntax. There are several changes as follows:
Replace PI()with ACOS(-1).
Since the name of temporary table cannot be the same as that of actual table, the name of temporary table is changed to A1, B1.
Substitute CONCAT(CONCAT(A_SN, ‘’), LISTAGG(B_SN,‘’) WITHIN GROUP (ORDER BY B_SN)) for CONCAT(CAST(A_SN AS VARCHAR(1000)), ‘’, GROUP_CONCAT(CAST(B_SN AS VARCHAR(1000)),‘’))
WITH A1 AS(
SELECT SN,
OnOrbitRA,
OnOrbitDec,
InputMAGG,
ACOS(-1)/180*OnOrbitRA RA,
ACOS(-1)/180*OnOrbitDec aDEC,
SIN(ACOS(-1)/180*OnOrbitDec) SIN_DEC,
COS(ACOS(-1)/180*OnOrbitDec) COS_DEC
FROM a
),
B1 AS(
SELECT SN,
OnOrbitRA,
OnOrbitDec,
InputMAGG,
ACOS(-1)/180*OnOrbitRA RA,
ACOS(-1)/180*OnOrbitDec aDEC,
SIN(ACOS(-1)/180*OnOrbitDec) SIN_DEC,
COS(ACOS(-1)/180*OnOrbitDec) COS_DEC
FROM b
),
T0 AS (
SELECT A1.SN A_SN,B1.SN B_SN,
B1.OnOrbitRA B_OnOrbitRA,B1.OnOrbitDec B_OnOrbitDec,B1.InputMAGG B_InputMAGG,
A1.OnOrbitRA A_OnOrbitRA,A1.OnOrbitDec A_OnOrbitDec,A1.InputMAGG A_InputMAGG
FROM A1 JOIN B1
ON A1.OnOrbitDec>=B1.OnOrbitDec-0.5/3600
and A1.OnOrbitDec<=B1.OnOrbitDec+0.5/3600
and A1.RA>=B1.RA-1.6548341646645552E-6
and A1.RA<=B1.RA+1.6548341646645552E-6
and (SQRT(POWER(B1.COS_DEC*SIN(A1.RA-B1.RA),2)
+POWER(A1.COS_DEC*B1.SIN_DEC-A1.SIN_DEC*B1.COS_DEC*COS(A1.RA-B1.RA),2))
/(A1.SIN_DEC*B1.SIN_DEC+A1.COS_DEC*B1.COS_DEC*COS(A1.RA-B1.RA)))
<=TAN((ACOS(-1)/180)*(0.3/3600))
),
T1 AS (
SELECT A_SN,B_SN,
B_OnOrbitRA,B_OnOrbitDec,B_InputMAGG,
A_OnOrbitRA,A_OnOrbitDec,A_InputMAGG,
ROW_NUMBER() OVER ( PARTITION BY B_SN ORDER BY A_SN ) RN
FROM T0
),
T2 AS (
SELECT * FROM T1 WHERE RN=1
),
T3 AS (
SELECT A_SN SN, 1+COUNT(*) CNT, CONCAT(CONCAT(A_SN, '_'), LISTAGG(B_SN,'_') WITHIN GROUP(ORDER BY B_SN)) SN_COM,
(A_OnOrbitRA+SUM(B_OnOrbitRA))/(COUNT(*)+1) OnOrbitRA,
(A_OnOrbitDec+SUM(B_OnOrbitDec))/(COUNT(*)+1) OnOrbitDec,
(A_InputMAGG+SUM(B_InputMAGG))/(COUNT(*)+1) InputMAGG
FROM T2
GROUP BY A_SN,A_OnOrbitRA,A_OnOrbitDec,A_InputMAGG
)
SELECT * FROM T3
UNION ALL
SELECT SN, 1 CNT, NULL SN_COM, OnOrbitRA, OnOrbitDec, InputMAGG
FROM A
WHERE NOT SN IN ( SELECT A_SN FROM T1 )
UNION ALL
SELECT SN, 1 CNT, NULL SN_COM, OnOrbitRA, OnOrbitDec, InputMAGG
FROM B
WHERE NOT SN IN ( SELECT B_SN FROM T1 );
VI. Test SPL
A
1 =now()
2 >radius=0.3/3600, delta_rad=0.5/3600, pi=pi()/180, std=tan(pi*radius)
3 =A=file(“A.csv”).import@tc(SN,InputMAGG,OnOrbitRA,OnOrbitDec).sort@m(OnOrbitDec) .derive@om(pi*OnOrbitRA:RA,pi*OnOrbitDec:DEC,sin(DEC):SIN_DEC, cos(DEC):COS_DEC,SN:AR)
4 =B=file(“B.csv”).import@tc(SN,InputMAGG,OnOrbitRA,OnOrbitDec).sort@m(OnOrbitDec) .derive@om(pi*OnOrbitRA:RA,pi*OnOrbitDec:DEC,sin(DEC):SIN_DEC, cos(DEC):COS_DEC)
5 =delta_ra=func(A11,B.max(abs(DEC)),std)
6 =B.derive@mo(OnOrbitDec-delta_rad:g, OnOrbitDec+delta_rad:h, RA-delta_ra:s,RA+delta_ra:e, A.select@b(between@b(OnOrbitDec,g:h)).select(RA>=s && RA<=e && (sqrt(power(COS_DEC*sin(B.RA-RA),2)+power(B.COS_DEC*SIN_DEC-B.SIN_DEC*COS_DEC*cos(B.RA-RA),2))/(B.SIN_DEC*SIN_DEC+B.COS_DEC*COS_DEC*cos(B.RA-RA)))<=std).min(SN):AR)
7 =(A|A6.select@m(AR)).groups@n(AR+1:SN; count(1):CNT, iterate(~~/“_”/SN,""):SN_COM, sum(OnOrbitRA):OnOrbitRA, sum(OnOrbitDec):OnOrbitDec, sum(InputMAGG):InputMAGG ).run@m(SN=SN-1, if(CNT==1,SN_COM=null,(SN_COM=mid(SN_COM,2),OnOrbitRA/=CNT,OnOrbitDec/=CNT,InputMAGG/=CNT)) )
8 =A7|A6.select@m(!AR).new(SN,1:CNT,null:SN_COM,OnOrbitRA,OnOrbitDec,InputMAGG)
9 =interval@s(A1,now())
A2: pre-calculate several constants.
A3-A4: read tables A and B; sort by OnOrbitDec; convert DEC and RA to radian, and calculate the sin and cos values of DEC in advance.
A5: calculate delta_ra.
A6: search table A by table B, and select the record with smallest SN once the records in table A are found, because the original order needs to be retained. Since the data in table A are sorted by OnOrbitDec in advance, the binary search is adopted in preliminary screening on OnOrbitDec, which can greatly reduce the amount of comparison calculation.
A7-A8: organize and calculate the matching records according to the required result table format, and merge the unmatching records in tables A and B into the result table at the same time.
VII. Test results
VM1 (Unit: seconds)
| Data scale | 10,000 rows | 100,000 rows | 500,000 rows |
|---|---|---|---|
| Starrocks | 5.87 | 211 | Error occurs after one hour |
| Oracle | 1.722 | 30 | 509 |
| SPL | 1.182 | 6.169 | 33.475 |
VM2 (Unit: seconds)
| Data scale | 10,000 rows | 100,000 rows | 500,000 rows |
|---|---|---|---|
| Starrocks | 8.15 | 423 | Not tested |
| Oracle | 1.526 | 30 | 511 |
| SPL | 1.072 | 5.637 | 45.863 |
In addition, we test SQL on VM1 without doing preliminary screening. The result shows that Oracle doesn’t get the result after running for 20 minutes when the data scale is 10,000 rows, while Starrocks gets the result after running for 5.86 seconds (almost the same as the time it spent on the task with the preliminary screening), and obtains the result after 9 minutes 49 seconds (much slower than the time it spent on the task with the preliminary screening) when the data scale is 100,000 rows. Overall, the preliminary screening makes sense for SQL.
VIII. Comments on test results
SPL Community Edition performs the best, far surpassing SQL-based databases.
It is quite strange that Starrocks, as a professional OLAP database, performs worse than Oracle even with the preliminary screening. The most likely reason is non-equivalence association, as such association operation cannot employ HASH JOIN algorithm, and has to resort to hard computing instead. It seems that the capabilities of these emerging databases are still insufficient for the optimization of complex calculations.
The reason why SPL performs best is mainly due to its ability to implement better algorithms, which will reduce the computing amount significantly. In contrast, SQL doesn’t have the ability to describe such stepwise operation, and cannot optimize non-equivalence association. Although the preliminary screening reduces a large portion of computing amount, the remaining amount is still large.
From the performance of SPL and Oracle, it seems that more CPUs do not work. After analysis, we believe that the possible reason is that the amount of data is small, and there are many duplicate data matched between multiple threads. In this case, the effect of more CPUs is not obvious.
Conclusions:For the unconventional computing tasks that SQL cannot optimize automatically, we can resort to SPL because it can help us code suitable algorithms with ease (in fact, SPL code is shorter and easier to develop), and the performance is much better than SQL.
Origin: http://c.raqsoft.com/article/1690526751007
SPL Source Code: http://c.raqsoft.com/article/1690526751007

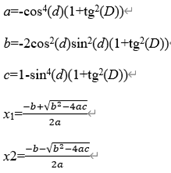

Top comments (0)