
Take my hand.
What are you afraid of?
Afraid of finding something out about yourself...?
Maybe even about the fabric of reality itself?
Let's see what lies at the center of this spiral.
Yes, of course, I'm talking about the spiral on my shirt.
What am I talking about? I don't know. It probably has something to do with the toy problem I worked on this week called: Spiral Traversal. I had a lot of fun solving this problem and I'd like to walk you through my journey.
First an explanation of the problem: given a matrix, return an array that traces all the values found in a spiral from the matrix's upper left corner into its center.
Here's a matrix:
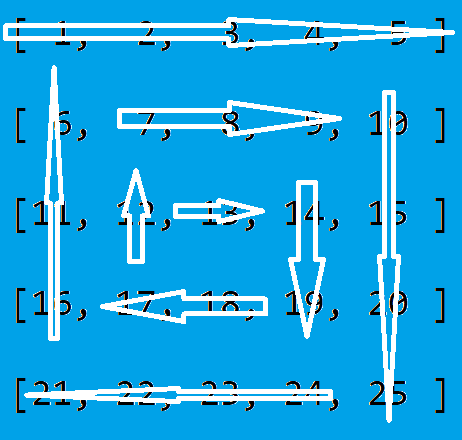
A spiral traversal looks something like this:
Writing that out, the array we'd want to return is:
[1, 2, 3, 4, 5, 10, 15, 20, 25, 24, 23, 22, 21, 16, 11, 6, 7, 8, 9, 14, 19, 18, 17, 12, 13]
Now that's a mouthful.
Let's take it step by step, following the diagram above. The first thing we want to do is grab the whole first row of the matrix and load it into our spiral. This could easily be accomplished by grabbing matrix[0] and pushing it into our spiral array. However, wouldn't it be nice to no longer have this row on the playing field moving forward? We can kill two birds with one stone by using shift.
let spiral = matrix.shift();
Because shift returns what it removes, we have now set our spiral equal to that first row. Now, we probably want our function to be pure, so we should make a copy of matrix before we rudely splice off part of it. The most obvious approach would be:
matrix = [...matrix];
However, if we think ahead a little bit, some parts of the traversal will only be grabbing PARTS of rows, which will mean altering the matrix's sub-arrays. These sub-arrays have their own references, so even if we make a copy of the matrix, any changes made to its rows will actually be side-effects. Knowing this, a more thorough approach is to make a copy of each row instead:
matrix = matrix.map(row => [...row]);
Now we are safe from accidentally altering both the matrix itself and any of its rows.
Let's get back to it. Our matrix now looks like this:
The next part of the traversal is down the right-most column (10, 15, 20, 25). So, we want to iterate through the matrix, popping off the last element of each row and tacking it onto our spiral.
matrix.forEach(row => {
spiral.push(row.pop());
});
Pop, like shift, returns what it removes, so we can push the elements into our spiral at the same time as we remove them from the matrix rows. Pretty cool!
Our matrix is getting smaller...
Up next we have to do a fancy little trick: add the bottom row...BACKWARDS! Actually, it's not that fancy because JS has a reverse method.
spiral = spiral.concat(matrix.pop().reverse());
Look at that cute little matrix:
Alright, next we need to traverse up the left-most column. So, we iterate BACKWARDS through the matrix, removing the first element of each row and adding it to our spiral.
for(let i = matrix.length - 1; i >= 0; i--) {
spiral.push(matrix[i].shift());
}
Wow! Our matrix is almost bite-size!
Cool! So...what next? Grab the first row from left to right, correct? Well...this is awkward. Aren't we about to repeat the same sequence of actions we just went through? What if we were dealing with a much larger matrix? How would we know how many times to repeat this sequence. We wouldn't! So let's recurse, like so:
return spiral.concat(spiralTraversal(matrix));
Easy enough. But what are our stopping conditions? Let's take a moment to visualize. When we call spiralTraversal on this 3 x 3 matrix, we will be performing this sequence:
So, when we get to the end of the sequence we'll be recursing again on the poor lonely 1 x 1 matrix: [ [ 13 ] ]. That 13 is totally the end of our spiral, so our stopping condition can be something like this:
if(matrix.length === 1) return matrix[0]
This stopping condition is essentially saying: if the matrix only has one row, go ahead and add that row as the end of the spiral. Now, up till now we've only considered square matrices. But let's consider a wide matrix and see if this stopping condition still works.
Starting matrix:
First traversal:
Matrix to recurse on:
We just want to tack this final [ 6 , 7 ] onto our spiral, and our base case will do just that. Looks like we're safe. How about a tall matrix?
Starting matrix:
First traversal:
Matrix to recurse on:
This matrix has only one column. Isn't safe we want the end of our spiral to be the contents of this column: [5, 8] ? We have one base case right now that says to add the whole row if there's only one left. How about we make another base case that says to add the whole column if there's only one left?
if(matrix.every(row => row.length === 1)) {
return matrix.reduce((col, row) => col.concat(row));
}
If every row in the matrix has only one element, that means there's only one column. We use the reduce to transform [ [5], [8] ] into [5, 8] for easy concatenation onto the end of our spiral.
Whew! All done, right? Wrong. We haven't considered one possibility: a square matrix with even-numbered dimensions! Let's visualize the simplest case.
Starting matrix:
First traversal:
Matrix to recurse on:
The first thing you might notice is that we didn't even get to complete our sequence on the first traversal! When it came time to traverse up the left-most column, there was already nothing left in the matrix. If you recall our code for this part of the traversal:
for(let i = matrix.length - 1; i >= 0; i--) {
spiral.push(matrix[i].shift());
}
We won't get an error, because i will initialize at a value of -1 (since the length is 0), meaning the loop never runs. After this, we call spiralTraversal on an empty matrix. Wouldn't you say we're done with our spiral though? I sure hope so. So it looks like we've found our final base case. If the matrix is empty we should just return an empty array to end it all.
if(matrix.length === 0) return [];
So now, if we put it all together with our base cases preceding our traversal sequence, it should look a something like this:
const spiralTraversal = (matrix) => {
//if matrix is empty, return empty array
if(matrix.length === 0) return [];
//if matrix only has one row, return that row
if(matrix.length === 1) return matrix[0];
//if matrix has just one column, return that column
if(matrix.every(row => row.length === 1)) {
return matrix.reduce((col, row) => col.concat(row));
}
//make a copy of matrix
matrix = matrix.map(row => [...row]);
//start with spiral set to the entire first row of the matrix
let spiral = matrix.shift();
//iterate through remaining rows, adding each row's final element to spiral
matrix.forEach(row => {
spiral.push(row.pop());
});
//add a reversed version of final row to spiral
spiral = spiral.concat(matrix.pop().reverse());
//iterate backwards through remaining rows, adding each row's first element
//to spiral
for(let i = matrix.length - 1; i >= 0; i--) {
spiral.push(matrix[i].shift());
}
//return the spiral so far, concatenated with a spiral traversal of the
//remaining matrix
return spiral.concat(spiralTraversal(matrix));
};
And that's it! Hope you enjoyed reading. See you on the other side...


















Top comments (0)