Algos - Searching & Sorting

algos stuff. summary sheet. Information here is all a combination from LeetCode & GeeksforGeeks

Summary: Big O Cheat Sheet

Searching

1. Linear Search
2. Binary Search
3. Jump Search

Linear Search

iterate through entire array, to search for intended item

Time Complexity: O(N)

Binary Search

searching for specific value in an ordered collection

• Target - value to search for
• Index - current location
• Left, Right - indices from to maintain search space
• Mid - index to apply condition to decide if search left or right

How it works

• Get middle index of sequence, apply search condition to middle index
• if unsatisfied / values unequal, half of sequence is eliminated
• Continue search in remaining half until target is found

Complexity

Recursion
Time Complexity: O(log(n))
Space Complexity: O(log(n)) (height of stack call, ~ height of binary tree)

Iterative
Time Complexity: O(log(n))
Space Complexity: O(1)

public int search(int[] nums, int target) {
    int left = 0;
    int right = nums.length -1;
    int midIdx = ((right - left) / 2 ) + left;

    while (left <= right) {
        if (nums[midIdx] < target) {
            // search in right half 
            left = midIdx +1;
            midIdx = ((right-left) / 2) + left;
        } else if (nums[midIdx] > target) {
            // search in left half
            right = midIdx - 1;
            midIdx = ((right - left) / 2) + left;
        } else {
            // nums[midIdx] == target
            return midIdx;
        }
    }
    return -1;
}

Jump Search

Check fewer items then linear search ( in sorted array) by jumping / skipping elements.

1. Search elements in array by index 0,m,2m etc.
2. find indexes where arr[k*m] < target < arr[(*k+1)m]
3. linear search from k*m till (*k+1)m to find target

optimal block size to skip

Time complexity = (N/m) + m
For minimum time complexity,
1 = (N/m) + m
1 - m = N / m
m - m² = N
m ~ sqrt(N)
Therefore, optional block size (m) is sqrt(N)

Complexity

Space Complexity: O(1)
Time Complexity:
assuming optimum block size m = sqrt(N),
Time Complexity = (N/m) + m
= (N/sqrt(N)) + sqrt(N)
= sqrt(N) + sqrt(N)
~ O(sqrt(N))

Sorting

Impt: understand trade offs for each algorithm

Elementary : n²

1. Bubble Sort (stable)
2. Insertion Sort (stable)
3. Selection Sort (stable)

More complex : n*log(n), divide and conquer

1. Merge Sort (stable)
2. Quick Sort (unstable)

depending on the type of input (eg. list is reversed / nearly sorted) algo will perform differently

For options 4 & 5. merge and quick sort utilize Divide and conquer. Divide and conquer gives log(n) advantage.

sort()

Java arrays.sort() uses dual pivot quick sort
complexity: O(n log(n))

Stable VS Unstable sort

Stable: objects with equal keys appear in the same order in sorted output as input.
** if two objects are compared as equal their order is preserved**

Taken from SO answer

When is stable sort required?
Stable sort is needed when equal elements are distinguishable.

e.g. multiple criterias for sort. sort by object.A THEN object.B

in stable sort. sort by object.B THEN object.A.

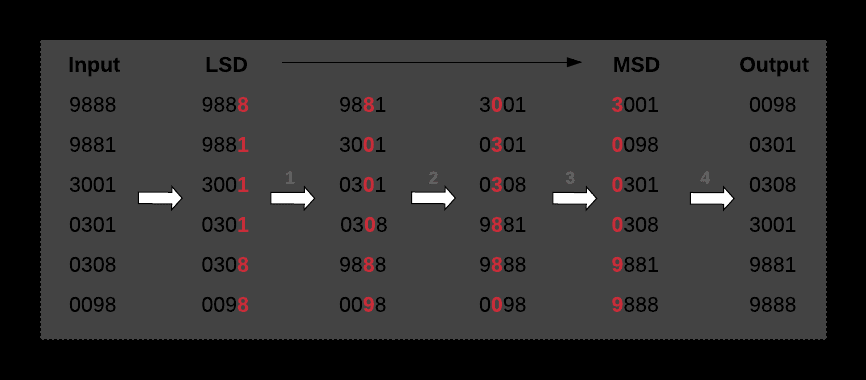
Eg. Radix sort.
sorting integers by digits that share the same significant position & value

1. Bubble Sort

repeatedly swap adjacent elements if they are in the wrong order

First pass brings max value to the end of array. second pass brings 2nd max value to second last index of array. To sort all indexes in ascending order need to do N passes. therefore complexity of n²

Time Complexity: O(n²)
Space Complexity: O(1)
Stable: yes

Input: 4A 5 3 2 4B 1
1st pass: 4A 3 2 4B 1 5
2nd pass:
3 4A 2 4B 1 5
3 2 4A 4B 1 5
3 2 4A 4B 1 5
3 2 4A 1 4B 5
3rd pass:
3 2 1 4A 4B 5
output: 1 2 3 4A 4B 5

2. Selection Sort

Find minimum element from unsorted part and putting it at the beginning. min element and element at beginning swap places.

First pass through unsorted part to get min value. Second pass through unsorted part to get second min value. N passes are needed to sort all elements in the unsorted part.

Time Complexity: O(n²)
Space Complexity: O(1)
Stable: no

Input : 4A 5 3 2 4B 1
Output :
1st: 1 5 3 2 4B 4A
2nd: 1 2 5 3 4B 4A
final: 1 2 3 4B 4A 5
swapping of places 4A and 1 made the selection sort unstable

Code example

void sort(int arr[])
    {
        int n = arr.length;

        // One by one move boundary of unsorted subarray
        for (int i = 0; i < n-1; i++)
        {
            // Find the minimum element in unsorted array
            int min_idx = i;
            for (int j = i+1; j < n; j++)
                if (arr[j] < arr[min_idx])
                    min_idx = j;

            // Swap the found minimum element with the first
            // element
            int temp = arr[min_idx];
            arr[min_idx] = arr[i];
            arr[i] = temp;
        }
    }

3. insertion Sort

best for: small dataset & nearly sorted data
array is virtually split into a sorted and an unsorted part. Values from the unsorted part are picked and placed at the correct position in sorted part. (compare one by one with elements in sorted part to find correct position).

class Solution {

  static void insert(int arr[],int i) {
      int num = arr[i];
      int insertionIdx = i;
      for (int j=i-1;j>=0;j--) {
          if (arr[i] < arr[j]) {
              insertionIdx--;
              if (j==0) {
                  break;
              } 
          }else {
              break;
          }   
      }
      for (int x=i;x>insertionIdx;x--) {
          arr[x]=arr[x-1];
      }
      arr[insertionIdx] = num;
  }
  //Function to sort the array using insertion sort algorithm.
  public void insertionSort(int arr[], int n) {
      //code here
      for (int i=1;i<arr.length;i++) {
          if (arr[i] < arr[i-1]) {
              int index = i-1;
              insert(arr,i);
          } 
      }
  }

}

Time Complexity
Best Case : O(n)
In best case, array already sorted, one pass, check that first element in unsorted part, is larger than last element in sorted part.
Worst & Average Case : O(n²
In worse case, array sorted in reverse order. algorithm will scan and shift through entire sorted subsection before inserting. will do this N times for all elements. so n²

Stable: Yes
Input: 4A 5 3 2 4B 1
Output:
1st pass: 1 4A 5 3 2 4B
2nd pass: 1 2 4A 5 3 4B
3rd pass: 1 2 3 4A 5 4B
4th pass: 1 2 3 4A 5 4B
output: 1 2 3 4A 4B 5

4. Merge Sort

Divide and Conquer algorithm
Divides the input array into two halves, (until each subarray is only size 2) calls itself for the two halves, and then merges the two sorted halves.

array is recursively divided into 2 halves until size is 1. Once size is 1, merge process starts and arrays are merged till complete array is merged.

Time Complexity: O(n*log(n))
Space Complexity: O(n)
Stable: yes

5. Quick Sort

best for: average complexity. Avoid if you cant garuntee a good pivot
Divide and conquer. Pick element as pivot point. Split array into two halves, lower than pivot element and higher than pivot element. Repeat process on subarrays until the halves have lenght of 1. Then combine all the elements back together to 1 array.

Time Complexity:
Best / Average : O (n*log(n))
Worst : O(n²)
worst case if the pivot point is the largest/ smallest element. List is not split into half.
Space Complexity: O(log(n))
Stable: no

Non-comparison Sort

Sorts are hard to beat O(n*log(n)) because you have to compare each element. to beat log(n) you need non-comparison sort

takes advantage of the way numbers (specifically integers) are stored in memory.

only work with numbers in a specific range

1. Radix sort
2. Counting sort

could be faster than merge or quick sort

When to use which sorting algo?

Insertion
few items / items are mostly sorted.
Bubble
Selection
Merge Sort

• best average and worst case is always O(n*log(n)) --> we will always divide up the list equally.
• if data set is big, suitable if you have external sorting (space complexity of O(n)) (data does not fit into main memory of computer device) Quick Sort
• avoid if you are scared of worst case (cannot garuntee good pivot)
• suitable if there is no external sorting. space complexity of O(log(n)) Radix / Counting Sort
• sorting integers

Trees & Graph - Searching

BFS VS DFS

BFS:

node is in upper level of tree

• shortest path / closest nodes
• more memory (need to keep tarck of current nodes)

DFS:

node is in lower level of tree

• less memory / does path exist?
• can get slow

Eg.

1. solution if not far from root of tree BFS

2. tree is deep, solutions are rare
   BFS (DFS will take long time) OR

3. tree is very wide
   DFS (BFS will need too much memory)

4. solutions are frequent but located deep in tree
   DFS

5. path exist between 2 nodes
   DFS

6. path exist between two nodes
   BFS

Djisktra & Bellman-Ford

shortest path between two nodes of weighted graph

• Bellman: can accommodate for negative weights
• Djisktra: more efficient but cannot accommodate for negative weights (greedy algo)

Djisktra cannot accomodate negative weights because it assumes "adding" a weight can never make a path shorter.