Algos - Complexity + Recursion

Summary for myself (from Leet Code explore card)

Analysis

Asymptotic

measure efficiency of function that dont depend on machine-specific constants

Guess run time of function in relation to the input size

Worst, Best, Average Case

Average case.

1. assumes all cases are uniformly distributed
2. calculate expected value Eg. linear search. Average complexity ~ O(n/2) ~ O(n) Full Explanation
3. assume that input is uniformly distributed
4. average case complexity = total number of comparisons made / number of inputs
5. element found on index 0, index 1, index 2, ... , index n
6. average complexity: = number of comparisons made / n = 1 + 2 + 3 + ... + n / n = (n* (n+1) /2 ) / n = (n+1) / 2 ~O(n/2) ~O(n)

Annotations

1. Theta (Θ) Notation --> upper and lower bound. (best & worst case)
2. Big O Notation --> upper bound (worst case)
3. Omega (Ω) Notation --> lower bound (best case)

Loops

1. O(1) no loop
2. O(n) loop, variable incremented by constant amount

for (int i = 1; i <= n; i += c) {  
        // some O(1) expressions
}

1. O(n^c) nested loops. c being the layers of nesting.

for (int i = n; i > 0; i -= c) {
       for (int j = i+1; j <=n; j += c) {
          // some O(1) expressions
}

1. O(log(n)) loop variables is divided / multiplied by a constant amount.

for (int i = n; i > 0; i /= c) {
       // some O(1) expressions
}

1. O(log(log(n))) loop variables is reduced / increased exponentially by a constant amount.

for (int i = 2; i <=n; i = pow(i, c)) { 
       // some O(1) expressions
}

1. **O(2²)

growth doubles with each addition to input data
often recursive algorithms by solving two smaller sub problems of N-1 SO answer

1. O(n!) adding loop for every element SO answer

Recursion

1. Recurrence Tree
2. draw recurrence tree
3. calculate time taken by every level of tree.
4. Master Method more details

Recursion

function calls itself

To avoid an infinite loop: rmb to have base case

Recursion functions usually consist of 3 parts

1. base case — terminating scenario that does not use recursion to produce an answer.
2. recurrence relation — set of rules that reduces all other cases towards the base case.
3. return - rmb to return things. usually there are two return statements one for base case and one for the recurrence relation.

In recursion, functions will get closer and closer to base case. When base case, function returns, and previous function calls are popped off the stack. If recurrence relation is not "returned" nothing is "returned" return type is void.

Complexity

This SO answer provides a quick analysis of time complexities of different recursion functions

Dyanmic Programming

Basically caching. Break problems down into sub problems.
Solve sub-problems only once and store their solution

1. can be divided into subproblems?
2. recursive solution
3. repetitive subproblems (like fibionacci, subproblems done over an over again) (use caching -> DP)
4. memoize subproblem

Memoization / Opti (Dynamic Programming)

optimize recursion problems by storing / caching previous functions. Preventing duplicate calls.

Eg. Fibionacci f(n) = f(n-1) + f(n-2)
In Fibionacci there can be multiple duplicate calls. (see below, duplicate calls are coloured same colour)

Complexity

Article provides more explanation

Time Complexity

Linear

Time Complexity = number of recursion invocations (R) and time complexity of 1 recursion call (O(s))
Time Complexity = R * O(s)

Example: Reverse String

printReverse(str) = printReverse(str[1...n]) + print(str[0])

Number of invocations = N (length of string)
Complexity of 1 invocation = O(1)
Therefore, time complexity = N * O(1) = O(N)

Execution Tree

Node = invocation of function. Therefore, number of invocations = number of nodes in tree (N_tree)
Time Complexity = number of nodes in tree (N_tree) * complexity of 1 invocation (O(s))
Time Complexity = N_tree * O(s)

This can also be used for linear. In linear, all nodes have 1 child and the number of nodes is the height of the tree.

The execution tree of recursion function will form an n-aray tree where n is the number of times recursion function appears in recursion relation

Example: Fibonacci
f(n) = f(n-1) + f(n-2)
recursion function appears twice in recursion relation. Therefore, execution tree is a binary tree.

Height of binary tree is N.
Number of nodes = number of nodes in binary tree of height N
= 2⁰ + 2¹ + 2² + ... + 2^N-1
= 2 ^N -1
~ O(2^N)

Therefore, time complexity
= nodes in execution tree * complexity of 1 invocation
= O(2^N) * 1
= O(2^N)

After Memoization

As mentioned previously, memoization optimizes complexity of recursion by minimizing duplicate calls. (i.e. reducing the number of children in the execution tree)

Example: Fibonacci
After memoization, duplicate calls are reduced. So
f(n) = f(n-1) + f(n-2) would now become
f(n) = f(n-1) + cache(n-2)

This is because result of f(n-2) would have been calculated in the previous invocation call f(n-1) where f(n-1) = f(n-2) + cache(n-3)
In optimized fibonacci, only f(n-1) must be calculated for calculation of f(n). f(n-2) is stored in cache. retrieving it from cache (hashmap) is constant operation.

Fibonacci = f(n) = f(n-1) + cache(n-2)
Recursion function only calls itself once. Nodes in Execution tree has 1 child. Recursion to calculate f(n) will be invoked f(n-1) times.

Time complexity
= Number of nodes in execution tree * complexity of 1 function call
= Height of execution tree * Complexity of 1 function call
= O(N) + O(1)
= O(N)

Space Complexity

Space complexity of recursion has 2 main components.

1. recursion related
2. non-recursion related

Recursion related

For normal function calls, space on stack is freed when function is returned. However in recursive functions, function (f2) calls another function (f1), so both functions are stored in stack. In recursive functions, functions will all be stored in stack until base case is base case is reached.

Space complexity = maximum depth of recursion tree

Stack Overflow

If stack allocated for program reaches maximum limit, program crashes.

Space complexity of recursion = Height of execution tree.

Non-recursion related

Space not directly relation to recursion. Eg.

1. storing global variables
2. saving intermediate result from recursion calls. (e.g. menoization: space complexity of hashmap from storing function call results)

Tail Recursion

** Java does not support tail recursion / tail call optimization

function is tail recursive if recursive call is last thing executed by function

This stackoverflow answer provides better details.

// non-tail recursive
function recsum(x) {
    if (x === 1) {
        return x;
    } else {
// non-tail because it does computation + recursive call
        return x + recsum(x - 1);
    }
}
// output
recsum(3)
3 + recsum(2)
3 + (2 + recsum(1))
3 + (2 + 1)
6

function tailrecsum(x, running_total = 0) {
    if (x === 0) {
        return running_total;
    } else {
// tail. only calls recursive function
        return tailrecsum(x - 1, running_total + x);
    }
}
// output
tailrecsum(3,0)
tailrecsum(2,3)
tailrecsum(1,5)
tailrecsum(0,6)
6

In tail recursive call, space is saved because, stack does not have to save space for every function call. Space is just "reused"

Stack allocated space for f(x₁) to call f(x₂). Then f(x₂) will call f(x₃). however stack wont have to allocate new space for f(x₂) it will just "reuse" the space if allocated for f(x₁).

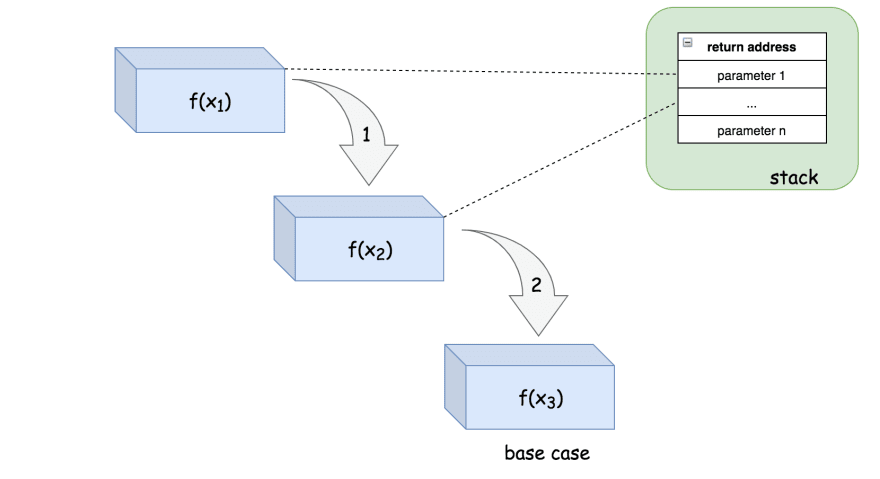
** Tail recursion calls can be executed as non-tail recursive functions** i.e. un-optimized stack space is used. This depends on programming language. Java and Python DO NOT support tail call optimization
Javascript ???

Recursive VS Iterative

• Readable: don't really have to repeat yourself.
• Large Stack: large stack call.

useful for traversal.

When to use recursion

using a tree / convergin something into a tree

Can Divide & conquer using recursion

1. Divided into number of sub problems that are smaller instances of same problem
2. each instance of sub problem is identical in nature
3. solution of each sub problem can be combined to solve problem at hand.

Sorting

1. Bubble Sort
2. Insertion Sort
3. Selection Sort
4. Merge Sort
5. Quick Sort

sort()

JS: under the hood, JS sorts list of numbers like string.
[1,2,35,67,7,8]
[1,34,65,7,2,8] -- > [1,2,34,65,7,8]