Data Structure - Linked List

My summary of Leet code linked list explore card. Additional information from GeekforGeeks

linear data structure.
Each element in the linked list is a separate object while all the objects are linked together by the reference field in each element.

1. Singly Linked List

Each node in a singly-linked list contains the value & reference field to link to the next node. This allows the singly-linked list organizes all the nodes in a sequence.

Node Strcuture

The first node in linked list is called head node
Head node if typically used to represent the whole list.

Each node in a list consists of at least two parts:

1. data
2. Pointer / Reference to next node

class LinkedList { 
    Node head; // head of the list 

   // constructor
   LinkedList() { head = null; }

    /* Linked list Node*/
    class Node { 
        int data; 
        Node next; 

        // Constructor to create a new node 
        // Next is by default initialized as null
        Node(int d) { data = d; } 
    } 
}

In Java or C#, LinkedList can be represented as a class and a Node as a separate class. The LinkedList class contains a reference of Node class type.

Operations

1. Find

complexity: O(N)
cannot access random element in constant time. to get to i ^th element must traverse from head to node one by one.

2. Add

2.1. Adding node at random location / after given node

complexity: O(1)

There is no need to move all elements past the inserted element (cur). In this case, prev node is given, just change "next" field.

1. check that given node is not null
2. initialize node to be inserted cur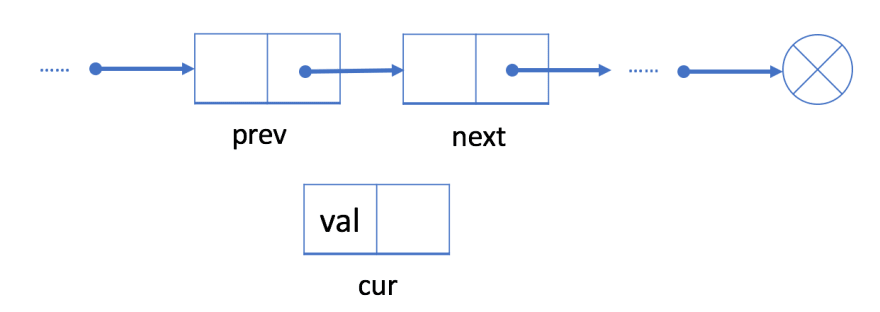
3. Link the "next" field of cur to node next
4. Link the "next" field in prev to cur

2.2. Adding node at front of Linked List

Since node head is used to represent the entire linked list. We need to

update head when adding new node to beginning of list

1. Initialize a new node cur
2. Link the new node to our original head node.
3. Move head to point to new node

2.3. Adding at end of linked list

complexity: O(N)

must traverse all elements of linked list to find last node

1. Create new node cur
2. Assign "next" field in cur to null.
3. if linked list if empty cur is head node
4. else, traverse linked list till the last node tmp is reached (node where "next field is null)
5. Link "next" field of last node to tmp to new node cur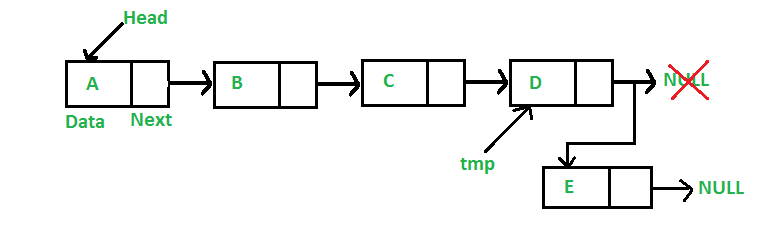

3. Delete

3.1 Delete a given node

time complexity: O(N)
space complexity: O(1)

eg. delete a current node cur

1. traverse linked list from head node to find previous node prev
2. Link "next" field in prev node to the next node

time complexity: O(N)
need to traverse linked list to find the node. time depends on number of nodes in linked list
space complexity: O(1)
need constant space to store pointers.

3.2 Delete head node

time complexity: O(1)

1. Assign head node as next node

3.3 Delete node at end of list

time complexity: O(N)

1. traverse through linked list till second last node prev is found
2. assign the "next" field of prev to null

Classic Problems

Cyclic Linked List

Check if linked list is a cycle

1. Hashmap

time complexity: O(N)
space complexity: O(1)
store past nodes in hashmap. check if next node is in the hashmap.

2. Two pointer

time complexity:
space complexity: O(1)
Get a fast runner and slow runner. if linked list is cyclic, fast and slow runner will eventually meet.

fast = node.next.next;
slow = node.next;

//check
if (fast == slow) {
    // list is cyclic
} 

Reverse Linked List

Reverse a singly linked list

1. Iterative method

time complexity: O(N)
space complexity: O(1)

Iterate through the nodes and move the to the head of the list one by one, until the original head node is the last one.

1. original
2. move second node to the head
3. move last node to the head original "head" node's next value is null. Algorithm can stop.

2. Recursive Method

Node reverse(Node head) {
  if(head == null) {
    return head;
  }

  // last node or only one node
  if(head.next == null) {
     return head;
  }

  Node newHeadNode = reverse(head.next);

  // change references for middle chain

  // next node after head, put forward and point to head
  head.next.next = head;
  // head will become tail so just make next null
  head.next = null;

  // send back new head node in every recursion
  return newHeadNode;
}

Time Complexity: O(n)
Space Complexity: O(n)
extar space from implicit stack due to recursion. Recursion can go n-levels deep

2. Doubly Linked list

Each node contains value field, next reference field & prev reference field

Node Structure

head node represents the entire linked list

class DoublyLinkedList{

   DoublyListNode head;

   // constructor
   DoublyLinkedList() {head = null;}

   class DoublyListNode {
      int val;
      DoublyListNode next, prev;
      // constructor
      DoublylistNode(int x) {val = x;}   
   }
} 

1. Find

time complexity: O(N)
Cannot access random position in constant time. must tarverse from head to ith node to access it.

2. Add

2.1 Add node after a given node

Time complexity: O(1)
Space complexity: O(1)

1. link cur's "prev" reference field with prev & link cur's "next" reference field with next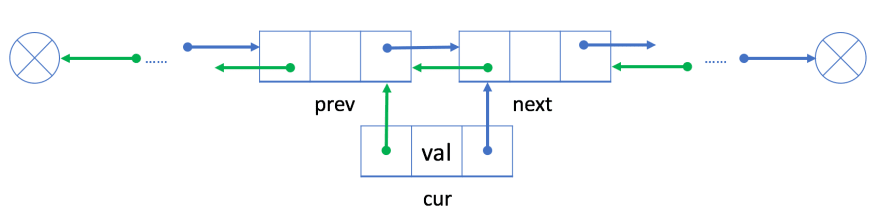
2. link prev's "next" reference field to cur & next's "prev" reference field to cur

2.2 Add node at head of list

time complexity: O(1)

1. Change cur node's next field to reference first node
2. Change first node's prev field to reference cur
3. Change head Node of doubly linked list to cur

2.3 Add node at end of list

time complexity: O(N)

1. Traverse linked list to find the last node of the list last (we only know head node from Doubly Linked List, must iterate to find the last node)
2. Change cur node's prev field to reference last node
3. Change last node's next field to reference cur node.

3. Delete

time & space complexity: O(1)
Can just link prev node's next field to cur node's prev field.

Can get previous node using prev field in doubly linked list

The ability to "go backwards" in doubly liked list means that there is no need to traverse linked list (O(N)) to get prev node

3.1 Delete a given node

time complexity: O(1)
space complexity: O(1)

eg. delete node 6

1. link 23's next field to 15
2. link 15's prev field to 23

3.2 Delete head node

time complexity: O(1)
space complexity: O(N)

1. Change head node of Doubly Linked List to second node
2. Change second node's prev field to null

3.3 Delete last node

time complexity: O(N)
space complexity: O(1)

still need to traverse to the end of linked list to get last node. So time complexity is O(N)

1. traverse linked list to find the last node end
2. Go backwards 1 step to find node second last
3. Change second last's next reference field to point to null.

Doubly VS Singly Linked List

taken from GeeksforGeeks

Advantage

1. bi-direction traverse

DLL can traverse both forward & backeard

2. delete more efficient

delete operation in DLL more efficient if pointer to node to be deleted is given

3. insert before given node

In singly linked list, to delete node, pointer to previous node is needed. So must traverse list.

Disadvantage

1. extra space

Every node of DLL requires extra space for previous pointer.

2. operations

All operations require previous node to be mantained. May require extra steps as compared to singly linked list.

Comparison with array

Advantage

1. Dynamic Size

Array size cannot be changed. So upper limit of elements must be known before creation.
Allocation memory for array is equal to upper limit irrespective of usage.

2. Better Complexity in insertion / deletion

Expensive because room must be created & existing items must be shifted.
Eg. sorted array
int[] id = new int[]{1000, 1010, 1050, 2000, 2040}
To insert new id (1005) & mantain order.
all elemented after 1000 must be moved
To delete id (1010), all elements after 1010 must be moved forward.

Disadvantage

1. Random access not allowed

Cannot be binary search with default implementation.

Binary search must find middle element then move left or right. in array its O(1) (get array.length/2) but in linked list, size is dynamic and must traverse elements to find length + get to middle element.

2. Extra memory space

For each element / node in Linked list, a pointer is required.
Each linked list Node must store its value + pointer to next node.

3. Not cache friendly.

Array is cache friendly since elements are placed right next to each other. however, elements of linked-list can be placed anywhere in the memory.
Therefore, iterating through linked-list will cause more cache miss since we cannot make use of locality of reference.

(Check out Cache operation - spatial locality. In Spatial Locality, memory in nearby locations are cached. different from temporal locality where actual memory is cached (often with a TTL - Time to live))

Summary

1. cannot access node in O(1) time
2. add node after given node / head in O(1) time
3. delete first head in O(1) time
4. deleting given node 4.1 singly linked list -> delete given in O(N) time, need O(N) time to find prev node 4.2 doubly linked list -> delete given node in O(1) time

Linked list better choice for adding / deleting nodes frequently. Array better if accessing random elements / nodes frequently.