Data Structure - Queue & Stack

Summary sheet for myself for Queue & Stack DS.
Resources from LeetCode & GeeksforGeeks

Queues & Stack can restrict processing order.

1. LIFO - Last In First Out
2. FIFO - First In Last Out

FIFO

First element added to the queue will be processed first

Operations

1. insert (enqueue) - item added to end of queue
2. delete (dequeue) - remove first element
3. rear - end of queue
4. front - front of queue

Queue - Implementation

Array implementation

ArrayList / dynamic array & an index pointing to head of the queue

class MyQueue {

    private List<Integer> data; //queue
    private int p_start; // head of queue 

    public MyQueue() {
        data = new ArrayList<Integer>();
        p_start = 0;
    }
}

Advantages

easy to implement

Limitations

Space wasted. when item is dequeued, head 'moves' forward and there is empty space at front of arraylist that is wasted.

Linked List Implementation

maintain two pointers front & rear (nodes of Linked List)

class MyQueue {
    QueueNode front, rear;

    // This function should add an item at
    // rear
    void push(int a)
    {
        // Your code here
        if (this.front == null) {
            this.front = new QueueNode(a);
            this.rear = front;

        } else {

            QueueNode addedItem = new QueueNode(a);
            this.rear.next = addedItem;
            this.rear = addedItem;
        }
    }

    // This function should remove front
    // item from queue and should return
    // the removed item.
    int pop()
    {
        // queue is empty
        if (this.front == null) {
            return -1;
        } else {
            int result = this.front.data;
            this.front = this.front.next;
            return result;
        } 

    }
}

Complexity
Time complexity for all operations: O(1) (no loops)
Space Complexity: O(N) for the linked list
Auxillary Space complexity: O(1) (extra space needed for operations)

Circular Queue / Ring Buffer

Array Implementation

resuses wasted storage space from array implementation

1. fixed size array
2. pointer - start position
3. point - end position

class MyCircularQueue {

    private int[] data;
    private int head;
    private int tail;
    private int size;

    /** Initialize your data structure here. Set the size of the queue to be k. */
    public MyCircularQueue(int k) {
        data = new int[k];
        head = -1;
        tail = -1;
        size = k;
    }   
}

• initial head & tail is null / -1. cannot be 0. because when queue has 1 element head == tail.
• queue is empty if head || tail is initial value (null / -1)

Complexity

Time Complexity
Enqueue O(1)
Dequeue O(1)
Front O(1)
Rear O(1)

Space Complexity
Space complexity: O(N)

Linked List Implementation

Queue in Java

In Java, Queue is an interface, concrete classes are Priority Queue or Linked list.

Priority Queues

allows users to process items based on priority

// Creating empty priority queue 
Queue<Integer> pQueue = new PriorityQueue<Integer>(); 

// Adding items to the pQueue 
// using add() 
pQueue.add(10); 
pQueue.add(20); 
pQueue.add(15); 

// Printing the top element of 
// the PriorityQueue 
System.out.println(pQueue.peek());

        // Printing the top element and removing it 
        // from the PriorityQueue container 
        System.out.println(pQueue.poll()); 

        // Printing the top element again 
        System.out.println(pQueue.peek()); 

Linked List

implements linked list data structure. Easier insertions / deletions make linked list preferred over arrays

// Creating empty LinkedList 
        Queue<Integer> ll 
            = new LinkedList<Integer>(); 

        // Adding items to the ll 
        // using add() 
        ll.add(10); 
        ll.add(20); 
        ll.add(15); 

        // Printing the top element of 
        // the LinkedList 
        System.out.println(ll.peek()); 

        // Printing the top element and removing it 
        // from the LinkedList container 
        System.out.println(ll.poll()); 

        // Printing the top element again 
        System.out.println(ll.peek())

Priority Blocking Queue

Priority Queue and Linked list are not thread safe. Priority Blocking Queue is thread safe.

// Creating empty priority 
        // blocking queue 
        Queue<Integer> pbq 
            = new PriorityBlockingQueue<Integer>(); 

        // Adding items to the pbq 
        // using add() 
        pbq.add(10); 
        pbq.add(20); 
        pbq.add(15); 

        // Printing the top element of 
        // the PriorityBlockingQueue 
        System.out.println(pbq.peek()); 

        // Printing the top element and 
        // removing it from the 
        // PriorityBlockingQueue 
        System.out.println(pbq.poll()); 

        // Printing the top element again 
        System.out.println(pbq.peek()); 

Applications

• items need not be processed immediately
• items processed in FIFO order (e.g. BFS)

Scenarios:

1. Resource shared among multiple consumers (CPU / Disk Scheduling)
2. data transferred asynchronously between two processes (response not receive at same rate as sent) (e.g. IO buffers, file IO, pipes etc.)

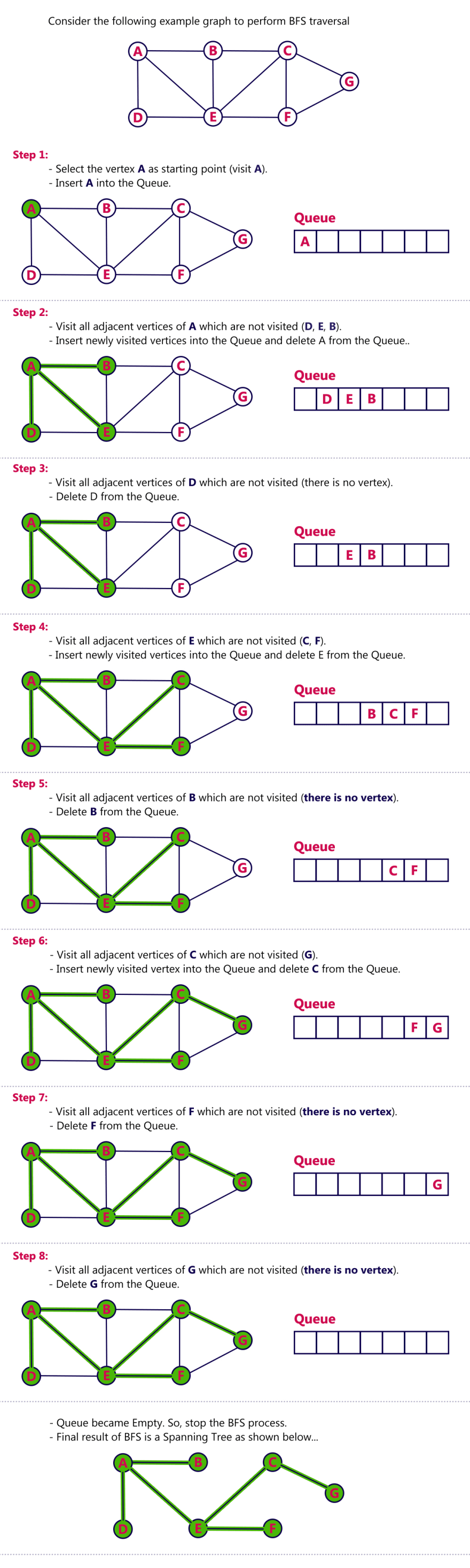
Queue & BFS

1. instantiate queue with length N (number of nodes)
2. start from root.
3. visit node and enqueue (add) it to queue
4. dequeue (pop) node from end of queue 5.1 visit all non-visited children nodes of popped node in 4 and enqueue them 5.2 if all child nodes are visited, delete node
5. repeat till 4-5 till queue is empty

process explained in more detail here
newly-added nodes are not processed immediately, they are processed in the next round (exact same process as queue)

NEVER visit a node twice, else one can get stuck in tree with loop (e.g. graph with cycle)

class Solution {
    //Function to return the level order traversal of a tree.
    Queue<Node> queue = new LinkedList<>();
    ArrayList<Integer> result = new ArrayList<>();
    ArrayList<Integer> levelOrder(Node node) {
        // Your code here
        queue.add(node);
        while (queue.size()>0) {
            Node top = queue.remove();
            result.add(top.data);
            if (top.left != null) {
                queue.add(top.left);
            }
            if (top.right != null) {
                queue.add(top.right);
            }
        }
        return result;
    }
}

Applications of BFS

1. Traversal
2. Find the shortest path

LIFO

newest element added to queue is processed first

Operations

1. push - add element to top of stack, if full then overflow
2. pop - remove element from top of stack, if empty its undeflow
3. peek / top - get top element of stack
4. isEmpty - check if stack is empty

Stack - Implementation

ArrayList Implementation

mantain top (for top of stack) & array

Linkedlist Implementation

Stack in Java

Java has a Stack class

// 1. Initialize a stack.
Stack<Integer> s = new Stack<>();
// 2. Push new element.
s.push(5);
s.push(13);
s.push(8);
s.push(6);
// 3. Check if stack is empty.
if (s.empty() == true) {
  System.out.println("Stack is empty!");
  return;
}
// 4. Pop an element.
s.pop();
// 5. Get the top element.
System.out.println("The top element is: " + s.peek());
// 6. Get the size of the stack.
System.out.println("The size is: " + s.size());

Stack and DFS

More details here

produces spanning tree (no loops)

1 Create an empty stack S.

1. Initialize current node as root
2. Push the current node to S and set current = current->left until current is NULL
3. If current is NULL and stack is not empty then 4.1. Pop the top item from stack. 4.2. Print the popped item, set current = popped_item->right 4.3. Go to step 3.
4. If current is NULL and stack is empty then we are done.

More details on the algorithm here