Big O Notation

Time complexity in computer science is the amount of time it takes for a machine to process an algorithm. Specifically we are interested in how processing time grows in relation to input size. Because processing time can differ for varying inputs of the same size, time complexity notation is factored considering a worst-case scenario. Since this can involve some very complicated mathematical computations, we use Big O notation as a shorthand for various levels of time complexity. Let's take a look at some of the common types of complexity we expect to see in programming, from best to worse performance.

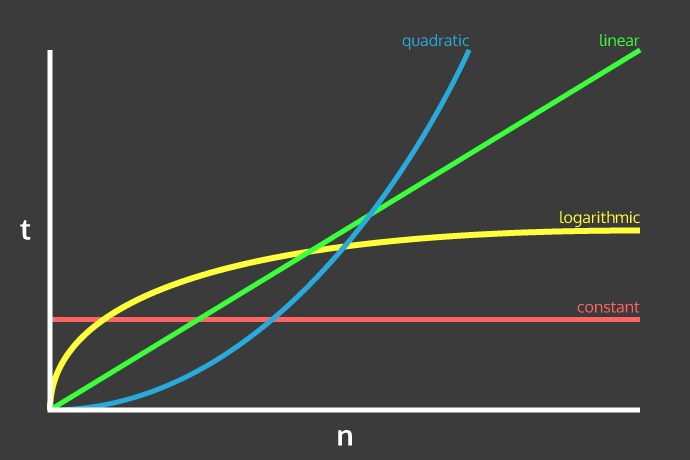
Constant Time O(1)

Constant Time means that no matter what the input size, the time it takes for the algorithm to run will remain the same. A familiar example of a constant time algorithm is looking up a value in an array at a known index.

Logarithmic Time O(log n)

Logarithmic Time means that as the size of your input grows, the processing time grows, but at an ever-reducing rate. A good example of this is a binary search tree. The reason for this being that the search field is reduced by half at every search cycle.

Linear Time O(n)

Linear Time means that as the input size increases, the processing time increases at a consistent rate. Common occurrences of linear time algorithms would be any function that may potentially have to loop over the entire input. Many higher-order functions such as map, filter, and forEach are examples of linear time algorithms.

Quadratic Time O(n^2)

Quadratic Time is when processing time increases at a rate which itself increases multiplicatively. Common examples of this are nesting a loop within a loop. Put in simpler terms, as input increases in size, processing time increases by the size of the input raised to some power.

Exponential Time O(c^n)

Exponential Time algorithms are when processing time increases exponentially as the size of the input grows. One common example of this is brute-force cracking of a password. This means that as input size grows, processing time increases by some constant raised to the power of the size of the input.

There are many other types of time complexity that we won't discuss here, but understanding these few examples is crucial in developing performant algorithms in your programs. We should all strive to improve the time complexity of our applications.