Does mathematics already scare you? Well, if it does take a deep breath and read on and by any chance if it does not, I will try my best to scare you now but ofcourse with a promise that we shall fill all the gaps before ending this post. Doesn't matter what programming langauge you code in, you shall still be able to relate to this post. For my convenience I will kill it with JavaScript.
So long back, I was working on a game that added 1 point to the user's score for every correct answer and deducted 0.1 points for a wrong one. The game starts with 1 point in your balance and then the score gets calculated based on your choices. Prima facie it worked fine (kind of) but then something caught me by dismay. I started the game (score = 1) and submitted three wrong answers back to back. What do you expect? A score of 1 - 0.1 - 0.1 - 0.1 = 0.7 ? Got you! Try that right away in your browser's console. It works alright you say? I bet you did 1 - 0.3, that indeed shall give you 0.7 but when you do it incrementally like I did, you shall see that
✔️ 1 - 0.1 = 0.9
✔️ 0.9 - 0.1 = 0.8
❌ 0.8 - 0.1 = 0.7000000000000001
Confused? Check out this codepen
Why is 0.8 - 0.1 not 0.7? Well, it is so in real world mathematics. So, is JavaScript's mathematics broken? Co-readers who also code in python would now tell you that even Python failed in its maths class. What's happening? Well, if you want a short blunt answer its the binary system making floating point calculations unpredictable. So yes its not your favorite programming language. We shall ofcourse discuss how to get around with this limitation but I cannot hold myself from digging a little more into the root cause.
Do we all understand that our computers store all and any kind of information in binary? Assuming you said 'YES', how is a decimal number (which we input) converted into binary before it gets stored? Do you know that after the number is converted into binary, to get stored in the register (memory), the binary should be first arranged in some appropriate format? "Binary Floating Point Representation" is the term we use for those formats. Call it FPR for simplicity.
Floating Point Representation
Binary Floating Point Representation can be of 3 types :
-
Half Precision Format
- available memory for a given number = 16 bits
- microFloat
- least precise & least wasteful
-
Single Precision Format
- available memory for a given number = 32 bits
- float data-type in Java
-
Double Precision Format
- available memory for a given number = 64 bits
- double data-type in Java
- most accurate representation of bigger numbers
Taking you back to school? No, please take a quick look (1.5x speed) at this video if you're not sure what did I just say. Now that you know we have limited space in the memory to store the binary representation, what if the binary of some number you input doesn't fit in 64 bits? Well, we round it up and make it fit in 64 bits somehow and hence we introduce the famous Rounding Error. This rounding error is the characteristic feature of floating-point computation and obviously when you input some number X, it may or may not stay exactly X after binary round off.
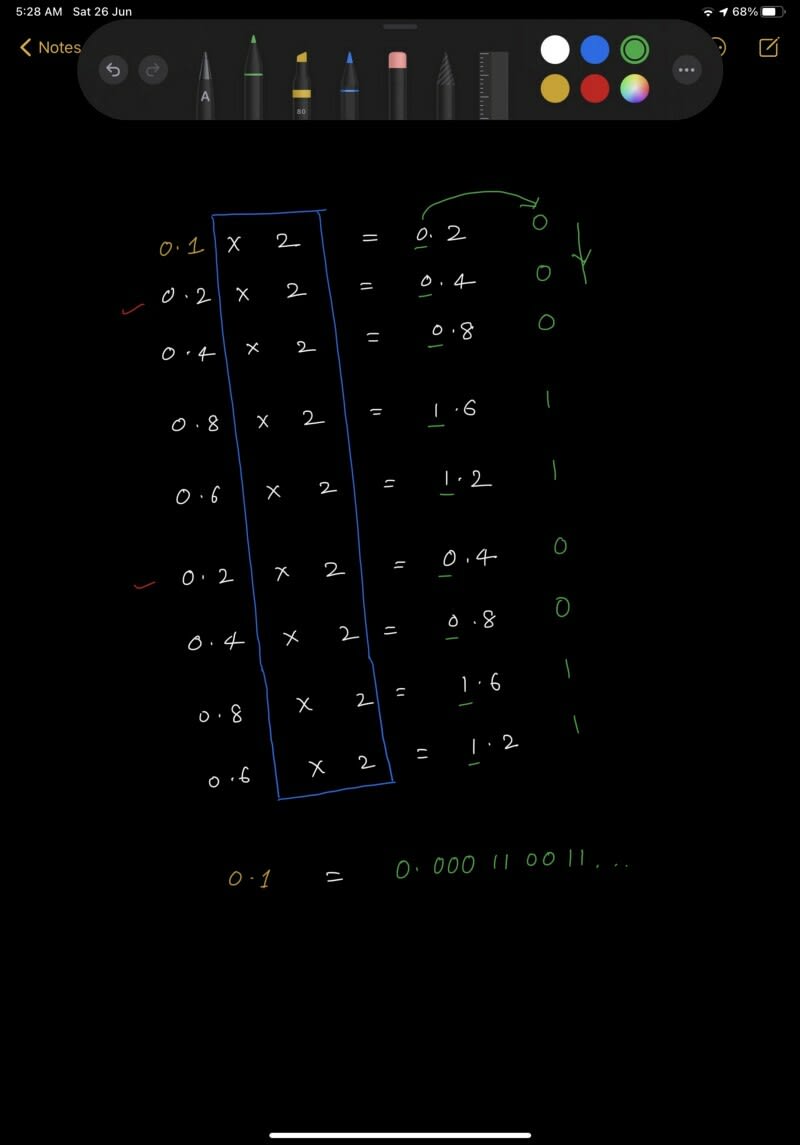
So what could be the examples of numbers whose binary won't fit even in 64 bits? A very obvious case can be of a number whose binary representation is non-terminating. 0.1 ? Seriously? Yes, lets see how this simple small decimal number has got a binary equivalent that never terminates (like the value of π in decimal).
Not my best handwriting though
That's how the decimal 0.1 looks in binary
There's a simple rule to find out if the given decimal number will have a non terminating binary or not. A decimal has an equivalent terminating binary if and only if the decimal, written as a proper fraction in lowest terms, has a denominator that is a power of two. Example : 0.1 has an infinite binary : 0.1 = 1/10, and 10 is not a power of two. Also 0.5, on the other hand, terminates: 0.5 = 5/10 = 1/2.
Apart from such numbers with non terminating binaries there can also be numbers with terminating but too big to fit in 64 bits binaries. Such numbers can also result in rounding errors. Now when I ask you to debug my game, you shall be able to atleast say (after looking at the output) that 0.8 - 0.1 is not 0.7 because somewhere in the binary round-off 0.8, 0.1 or 0.7 or maybe all of them got introduced to the rounding error. So what do we learn from this? We learn that FPR of the decimal numbers we input can make calculations unpredictable. How do we deal with this? Well, I shall tell you how, atleast how in JavaScript.
Solution to the round-off error in JavaScript
- Math.round((0.8-0.1)*factor)/factor shall give 0.7, where factor = 10 for rounding to single digit, 100 for rounding the result to 2 digits after decimal and so on.
- (0.8-0.1).toFixed(1) shall give "0.7" but in string format. Mostly irrelevant now but "toFixed" may show inconsistencies amongst older versions of some browsers. Read more.
- There can be many more solutions. For example the "floor" and "ceil" functions of the Math object depending on the use-case or even custom functions like so.
Conclusion
Most decimals have infinite representations in binary. Due to limitation of memory, rounding errors may get introduced in numbers whose binary equivalent does not fit even the Double Precision Format. So do not be surprised the next time you see an anomaly in floating point calculations. Its good to use one of the above mentioned solutions or a custom tailored solution that fits your requirement.
Originally posted here -
https://mayankav.webflow.io/blog/javascripts-broken-mathematics







Top comments (0)