Till now we have learned about nodes
Now, we will learn what is tree and all. First transform this node to a binary tree

Now, lets see how to form a binary tree

This is a full tree because each node has 2 nodes or values with it. node 7 & 12 has pointed to None which is invisible here.
Now

this is a Perfect Tree (Equal in both sides)
now,

Imperfect but full tree.
Also, this is a Complete tree because there is no within nodes. Every node has something.

but

this is Complete because there was no gaps in the tree but not full because node 12 has just one node 8 with it . And also not Perfect because it is not equal in both sides.
Moreover,

this is full because every node has 2 nodes with it and also Complete because it is filled and no gap in nodes.
again,

this is full because every node has 2 nodes along with it . Also Perfect because equal in both sides and also Complete because there is no gap.
Parent and Child & Leaf
Every node must have just 1 parent .

Also, nodes that don't have children are called leaf
Binary Search Tree
Let's learn what is Binary Search Tree. Let's have 2 nodes:
Now, the 2nd node 76 is bigger than 47, right? so, why are we comparing right?
Okay! If the 2nd node is bigger than 1st node, we will keep it to the right side .
B
But, if the 2nd node would have been smaller than 1st one, we would have set it to the left side.

But as 76 node is bigger than node 47, ultimately it will be:

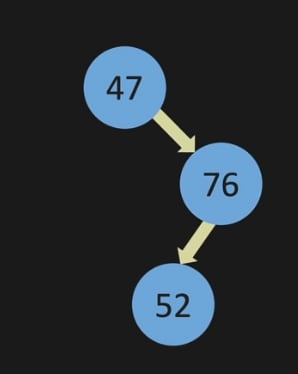
Now,let's have a 3rd node 52:
We will start comparing from the node at the top 47,

As 52 is greater than 47, it is going to be in the right side. But 47 has a node 76 in right side.

Now, we will compare 52 with node 76. As 52 is less than 76, it will be in the left side.
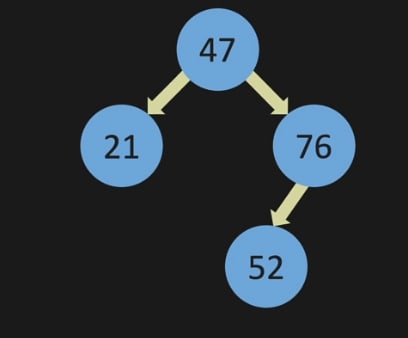
Let's have another node 21. Again, we will start comparing it from the top node 47.

As 21 is less than 47, node 21 will be on the left side. also, 47 has no node in left side and thus , it will easily seat in the left side

Now , 82 is bigger than 47 thus it will be in the right side of 47. There is a value in right side of 47, thus we can not remove it. Rather comparing with it. 82 is bigger than 76 too. Thus it will be in the right side of 76.
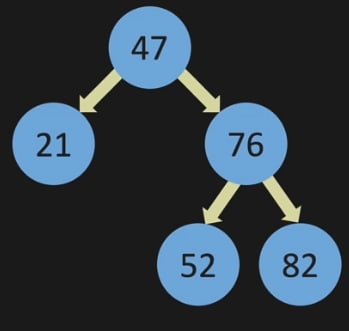
Also while adding 18 & 27, assume where are they going to be !
Binary Search Tree Big O
Here in 1st level linked list,

2nd level linked list,
We can skip 1 and take 2^1, 2^2,2^3,2^4 etc in count.
Something like this:
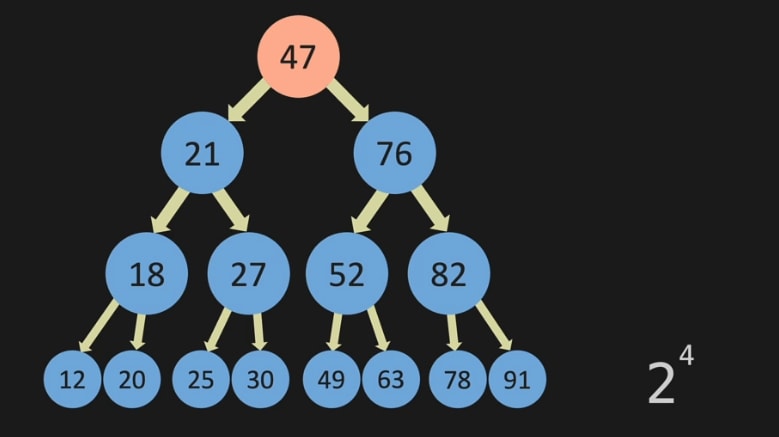
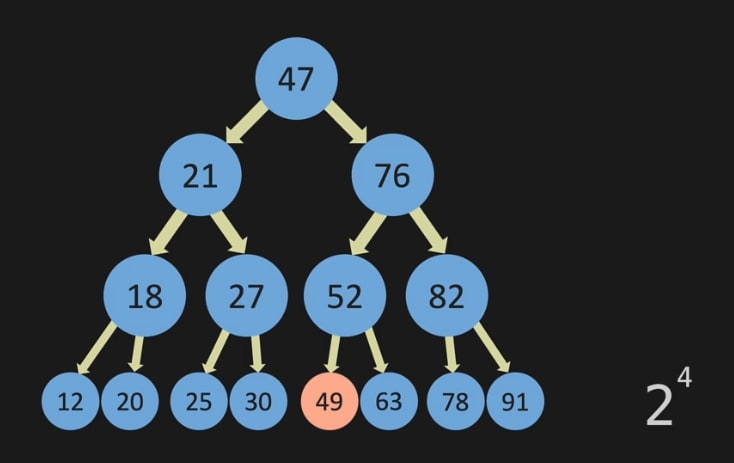
Here, if you look for the number 49, it took 4 steps (47->76->52->49)
as , we have now 2^4 nodes and it took 4 steps .
Note: we skipped 1 , as it is not that significant (2^4 -1)
Also, you will see that it took 4 steps to remove something and add something.
Therefore , it is O(log n) which is very efficient
O(log n ) is achieved by divide & conquer.
for lookup(), insert() & remove() it is O(log n)
Comparing it to Linked List, to lookup(), it is O(n) because you need to iterate through the list
but, to insert something it is O(1)

because you just need to add a node.
In this case it is only better than Binary Search Tree.
Constructor
We will have a node class
because it is
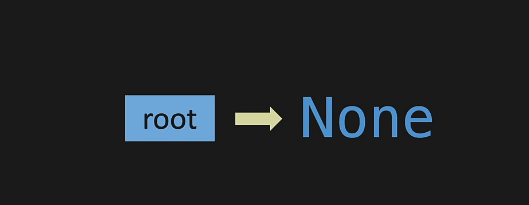
In tree, we have something called root which points to the first node
But , we are not going to use it. We are going to create an empty Binary Search Tree

And this will be our constructor primarily.
class Node:
#creating a node
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class BinarySearchTree:
def __init__(self):
self.root = None #Creating an empty BInary Search Tree
#Creating a Binary Search Tree
my_tree = BinarySearchTree()
print(my_tree.root)
Insert
First we will create a node

Case 1:
When we have nothing in the Binary Search Tree, we will just add that to root
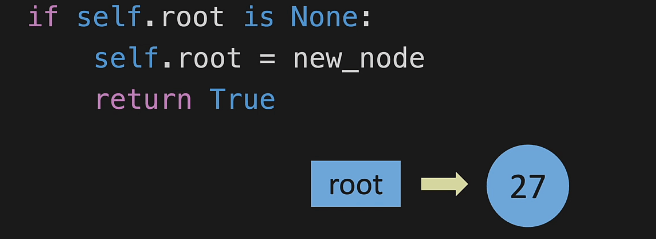
We will also set root as temp so that we can try different things.
Case 2:
If a node already exists in the BST( Binary Search Tree) , we can not add it.

For example, we have node 76 to insert in the BST but node 76 already exists, so we will return False and not initiate it.
Case 3:
It is when we have BST and also a new node and we will compare.
Here new_node.value is 18 and we will compare it will temp.value which is 47. if 18 is less than 47, it will be moved to left and if 18 is bigger than 47, it will be moved to right.
here, 18 is less than 47 and thus it will be moved to left .
now, we will check if there is already a node there or not. If there is no node, we will add 18 there.

But , if there is already a node , then we are going to change the temp.value and start comparing it again.

This will continue to work because it is within a while loop.
Same case for the right side.
adding 82 node in BST

as 82 is bigger than 47 and the right side was empty, it will be inserted there
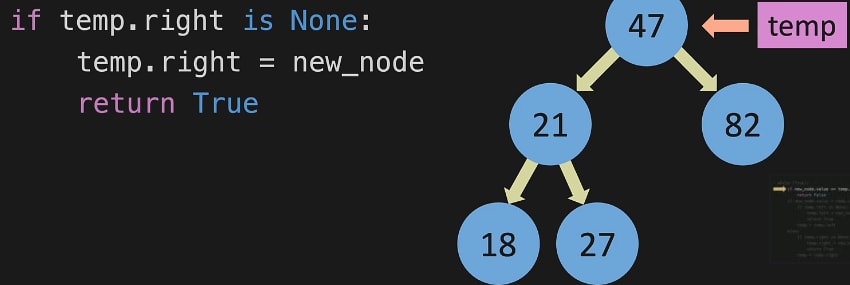
but, there is already a node there, we will just change the temp.value and follow the process again.
SO, that is how we will insert a value.
The code:
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class BinarySearchTree:
def __init__(self):
self.root = None
def insert(self, value):
#Creates a node
new_node = Node(value)
#Checks if the BInary Search Tree is empty or not. If empty, then adds the node there
if self.root is None:
self.root = new_node
return True
#starts working from the root to compare with the node
temp = self.root
while (True):
#Checks if the node that we want to insert already exists
if new_node.value == temp.value:
return False
#Checks if the node is smaller than the temp value
if new_node.value < temp.value:
#Checks if the left side of the temp value is empty or not
if temp.left is None:
temp.left = new_node
return True
#if not empty
temp = temp.left
else:
#Checks if the right side of the temp value is empty or not
if temp.right is None:
temp.right = new_node
return True
#if not empty
temp = temp.right
#Creating a BST
my_tree = BinarySearchTree()
#Inserting node 2 in the empty BST and thus the node 2 will be appointed as root & also temp value
my_tree.insert(2)
#First it will check if node 1 already exists or not
#Inserting node 1 . FIrst we will check if that node 1 is less than node 2 and then it will be moved to left
#temp.left= node 1
#as node 2 has nothing in left , that's why it will be added to left side
my_tree.insert(1)
#FIrst it will check if node 3 exists or not
#now node 3 is greater than 2 and thus temp.right will be node 3
#as there is nothing in right side of node 2, node 3 will be added.
my_tree.insert(3)
print(my_tree.root.value)
print(my_tree.root.left.value)
print(my_tree.root.right.value)
Contains
We are going to look for a node if it exists or not.
if we are looking for a node and we find that the Tree then surely the node is not in there:

now assume that we are looking for node 27 and 27<47 (temp) and thus we will change the temp to 21 which is in the left of previous temp (47)) and look for the 27 again.
If we were looking for 82, then 47 (temp) <82 thus we will change the temp to the right value 76 and look for 82 again
Now , when we will reach to our desired 82 or 27, we will see that the node we were looking for has been found . Thus, we will return True.

Also, when we will not find our desired node, we will return False.
That's it.
The code:
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class BinarySearchTree:
def __init__(self):
self.root = None
def insert(self, value):
new_node = Node(value)
if self.root is None:
self.root = new_node
return True
temp = self.root
while (True):
if new_node.value == temp.value:
return False
if new_node.value < temp.value:
if temp.left is None:
temp.left = new_node
return True
temp = temp.left
else:
if temp.right is None:
temp.right = new_node
return True
temp = temp.right
def contains(self, value):
#Setting the root value as temp
temp = self.root
while (temp is not None):
#Checks if the node is smaller than the temp node
if value < temp.value:
temp = temp.left
#Checks if the node is bigger than the temp node
elif value > temp.value:
temp = temp.right
#Checks if the node is equal to temp node
else:
return True
return False #When temp is None, it will return False
my_tree = BinarySearchTree()
my_tree.insert(47)
my_tree.insert(21)
my_tree.insert(76)
my_tree.insert(18)
my_tree.insert(27)
my_tree.insert(52)
my_tree.insert(82)
#Looking for 27 in the tree
print(my_tree.contains(27))
#Looking for 17 in the tree
print(my_tree.contains(17))
Minimum value
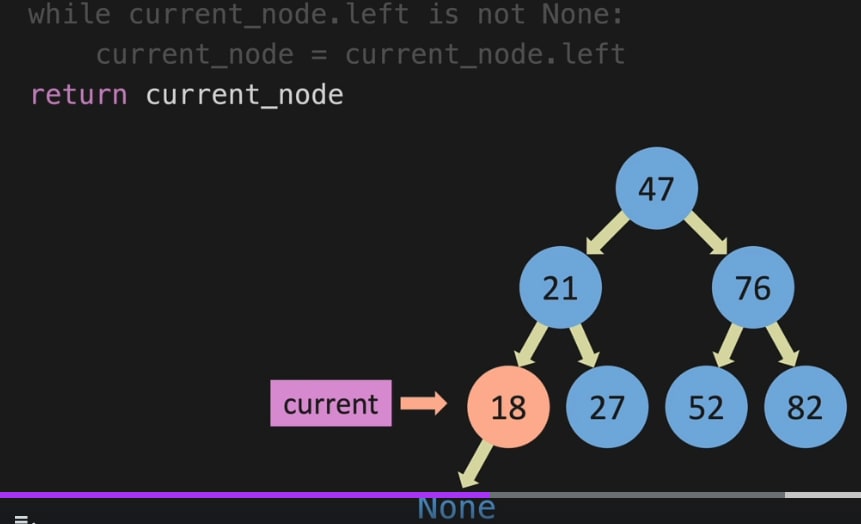
Looking for the minimum value in the Tree.
Here we will just check the left side untill we get None. We will return the node which has the None in its left side.

If not None, it will move to the left value

When we get the None, we return the current node
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class BinarySearchTree:
def __init__(self):
self.root = None
def insert(self, value):
new_node = Node(value)
if self.root is None:
self.root = new_node
return True
temp = self.root
while (True):
if new_node.value == temp.value:
return False
if new_node.value < temp.value:
if temp.left is None:
temp.left = new_node
return True
temp = temp.left
else:
if temp.right is None:
temp.right = new_node
return True
temp = temp.right
def contains(self, value):
#Setting the root value as temp
temp = self.root
while (temp is not None):
#Checks if the node is smaller than the temp node
if value < temp.value:
temp = temp.left
#Checks if the node is bigger than the temp node
elif value > temp.value:
temp = temp.right
#Checks if the node is equal to temp node
else:
return True
return False #When temp is None, it will return False
def min_value_node(selrf,current_node):
while current_node.left is not None:
current_node=current_node.left
return current_node
#enter current_node.value to see the value
my_tree = BinarySearchTree()
my_tree.insert(47)
my_tree.insert(21)
my_tree.insert(76)
my_tree.insert(18)
my_tree.insert(27)
my_tree.insert(52)
my_tree.insert(82)
print(my_tree.min_value_node(my_tree.root))#the count starts from root 47
print(my_tree.min_value_node(my_tree.root.right))#here the count starts from root.right which is 76
Pre order code , In Order & Post order tree traversal
Check out more
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.val = key
# A function to do inorder tree traversal
def printInorder(root):
if root:
# First recur on left child
printInorder(root.left)
# then print the data of node
print(root.val),
# now recur on right child
printInorder(root.right)
# A function to do postorder tree traversal
def printPostorder(root):
if root:
# First recur on left child
printPostorder(root.left)
# the recur on right child
printPostorder(root.right)
# now print the data of node
print(root.val),
# A function to do preorder tree traversal
def printPreorder(root):
if root:
# First print the data of node
print(root.val),
# Then recur on left child
printPreorder(root.left)
# Finally recur on right child
printPreorder(root.right)
# Driver code
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print "Preorder traversal of binary tree is"
printPreorder(root)
print "\nInorder traversal of binary tree is"
printInorder(root)
print "\nPostorder traversal of binary tree is"
printPostorder(root)



























Top comments (0)