Given a string abc, our goal is to generate the following unique substrings:
['abc', 'bc', 'ab', 'c', 'b', 'a']
With A Queue
We can do it with the help of a queue.
Here's the logic:
- Take the given string, add it to our queue
q. - While the
qis not empty, repeat steps 3-5. - Pop the first item in the
q. - Add this to our final result list called
res. - Add left substring (e.g.
ab) and right substring (e.g.bc) to the queue only if it isn't already inres. - Once queue is empty, print
res.
def findSubstrings(s):
res = set()
q = [s]
while q:
s = q.pop(0)
res.add(s)
x = 0
y = len(s)-1
right_string = s[x+1:y+1]
left_string = s[x:y]
if right_string and right_string not in res:
q.append(right_string)
if left_string and left_string not in res:
q.append(left_string)
return res
r = list(findSubstrings('abc'))
r.sort(key=len, reverse=True)
print(r)
# Result:
# ['abc', 'ab', 'bc', 'b', 'c', 'a']
With Recursion
Here the logic is the same but we do it recursively using one helper function.
def findSubstrings(s):
res = set()
def helper(s):
if len(s) <= 0:
return
res.add(s)
right_string = s[1:len(s)]
left_string = s[0:len(s)-1]
if right_string not in res:
helper(right_string)
if left_string not in res:
helper(left_string)
helper(s)
return res
r = list(findSubstrings('abc'))
r.sort(key=len, reverse=True)
print(r)
# Result:
# ['abc', 'ab', 'bc', 'b', 'c', 'a']
Complexity
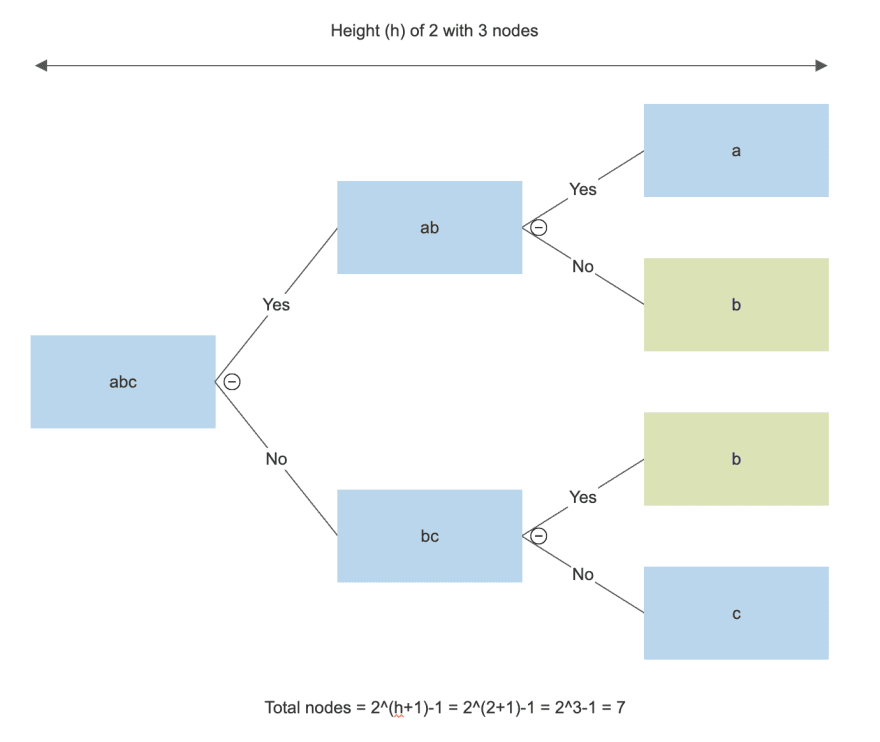
I guess the worst case time here could be (2^n)-1 if we don't use a set to check for unique values (where n is length of the given string).
Final Thoughts
Where can you use this? Once you understand the basic logic, you can use it to solve many string related problems. For example: Finding the longest palindromic substring.
There could be various other (simpler) ways to achieve this but I believe this approach helps us visualize the process. Thanks for reading! :)


Top comments (0)