As programmers, we often want our code to be DRY - written with the fewest characters possible. However, as anyone who has been stuck in a death loop of recursion can attest, even syntactically DRY bits of code can cause us problems:
def death_loop(num)
return death_loop(num + 1)
end
But what if our code needs to be recursive? Sometimes we need to write functions that call on themselves.
Enter memoization.
Memoization is an optimization technique used primarily to speed up computer programs by storing the results of expensive function calls and returning the cached result when the same inputs occur again.
In other words, memoization offers programmers the chance to be DRY functionally as well as syntactically, reducing the number of times a function is called by our program.
How it works
We will define a function. Let's call it compute(input)
In the body of the function, compute(input) will...
- Check if this precise input has been computed before (using a
memovariable we will define below). - If this input has been computed before, return
memoand save the program needless computing! - If this input has not yet been computed, perform computations.
- Save result of the computations to
memo. - Return the result.
Let's take a look at a case that's a little less common and a little more interesting than a recursive death loop.
Enter Fibonacci
If you were an enthusiast of calculus or the illuminati in high-school, you may have encountered that most famous example of recursive sequences, the Fibonacci Numbers. Put simply, each number in the sequence (integers only) is equal to the sum of the two preceding numbers, starting with the bottom two numbers of 0 and 1.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... and on to infinity.
Let's take a look at Fibonacci in code. Written in Ruby without memoization, our Fibonacci code might look something like this:
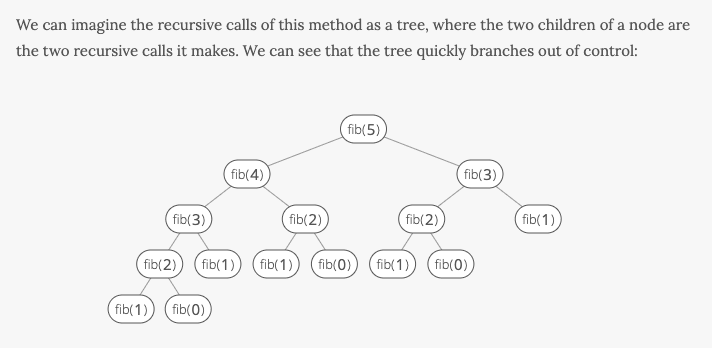
This solution works great for small numbers, but comes with some serious time complexity costs. As the input increases, the "sub-calls" of our function grow exponentially, as illustrated by a recursion tree:
To save on these costs, we can define a Memoize class in Ruby and use a @memo variable to cache our completed computations.
Benissimo. Fibonacci memoized.






Top comments (0)